CBCTF 第三届赛博杯

2020-07-28 match 2020赛 ∞ 评论

从群友@Neve3no处得知并打打酱油的小赛~~

Misc

66 6c 61 67 7b 39 35 63 35 62 66 33 32 32 39 32 64 37 35 66 35 37 61 35 30 36 37 36 66 36 61 62 35 64 64 38 33 7d

直接hex转string得flag。

α层

这波啊，这波在阿尔法层

用stegsolve工具将两张图片xor操作，圈中正确flag。

guess

有些事，看得很清，却说不清；有些人，了解很深，却猜不透；有些理，很想不通，却行的通。
地址：47.52.113.129 12345

猜数字，误差值小到0.001的值算成功。先输入给的值，然后到轮自己给数，输入范围0.00-10000.00内任何一个数，脚本二分法猜测最坏情况都能在 $\log_2{10000*100} \approx 19.9$ 次猜出。

考虑特殊数值NaN，用来表示一个本来要返回数值的操作数未返回数值的情况。任何涉及NaN的操作都会返回NaN，其次，它与任何值都不等，包括自身。

输入nan，脚本猜测次数超过20，拿到flag。

Web

尖尖的商店

尖尖开了一个商店,快看能不能买到flag吧 http://checkin.race2020.0rays.club/

一个购买页面，余额1000不足以购买99999价值的flag。抓包发现余额值存储于cookie里的money中，直接修改提交请求，拿到flag。

Hacked_By_V

V今天看到了一个弱口令的站，反手就把他日了。听说后台密码是admin/123456 http://47.52.113.129:10002/
链接：https://pan.baidu.com/s/1FL7scmbbEvIP3wskLVGVOw 提取码：1234

易居CMS（EjuCMS），下载源码，版本2.x，给了后台账密。首先搜索现成漏洞，存在后台模板代码执行漏洞。

找到后台/login.php?s=Admin/login进入，功能模块-模板管理-default管理，随便找一个文件，如 pc下的list_search.htm，显然能知道此为搜索结果页模板，执行代码部分都位于花括号{}中，尝试插入{php}phpinfo();{/php}保存，前端发现能成功执行。（可在目录下根据时间查看他人修改痕迹2333~）

一开始将代码修改为{php}echo system('ls');{/php}发现执行不成功，回到phpinfo结果页查看disable_functions，看到passthru/exec/system/putenv/shell_exec全不能使用。

换读取函数上，修改代码为{php}print_r(scand_dir('.'));{/php}读到目录下flag文件flag_BzH652，再用{php}print_r(file_get_contents('flag_BzH652'));{/php}读出flag。

Crypto

check_in

关于这道题，我听过一个及其诡异疯狂的谣言，在那漫长到无法计算的岁月之前，这道题就已经存在了。

from gmpy2 import *
from sympy import isprime,nextprime
from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse
from vanish import flag
import random


def Getprime(g):
 while True:
     p=g*random.randint(1,g)+1
     if isprime(p):
         return p

m=bytes_to_long(flag)

g=getprime(512)
p=Getprime(g)
q=Getprime(g)

e=65537
def lcm(a,b):
 return (a*b)/gcd(a,b)

print 'lcm(p-1,q-1): %d'%(lcm(p-1,q-1))
print 'n: %d'%(p*q)
print 'c: %d'%(pow(m,e,p*q))


'''
lcm(p-1,q-1): 29222879530390785742605477742453420902991175027283185502224574005903986263169096240656898659768251131170153243355896585116206546809026765977240398343841844413932022486239027317290376878970267549705130293352356070399197681533774641809920245792277386418338948725614463605422608450981946445029718369662946357705499281823362508397007696635982211082237545037851621498721235291885337720080893169582699780294708804334786758878624750037193583886404728146815380945201540
n: 2228582814888322539771891137733971181257097900700884269780928959802985615275288341111620316685788511492461651695428697100554113037555468881895905318207963274537589532345166133820089694201148988443496514751074857966136041157336680322417272183777409351597268908625677512781049274972325769500959755298004643407023188886359792411648183582888979219785653927285023667015990929441992061367448365123092899330885934801013411132173550954938961520075931155848843991824723727187297663420031211934554344568933171179175237722716971390081142435747796272698118097337803559316319210494963021258386613285360239662354953552369582646607
c: 2201106853018581355094419701171997731036843750081916703504266002782698731288317690546242336345890702261049147276084047271293227314969153138029180802403349980519050857699472720333400348342466190619778247784674359271736569275019018808569614566880813745619585529292155639979431043005511905548345767685472340763230813956617014122768477272236518467064016133244646900977041959848793579834848773548018337874928875046550721154575652528641850315494384644468806058021812603748441246192757443085386516155814337307681275922473564325028703523754319072117202083218199961250157611091952832038366393322275194833927035639232266868638
'''

由于 $lcm(p-1,q-1) =k(p-1)(q-1)<< n=pq$，求 $d$ 时用的模如为常规的 $\varphi(n)=(p-1)(q-1)$ 则 $k$ 的爆破空间将很大，所以用的模应是 $\lambda(n)=lcm(p-1,q-1)$。再按常规解 $m$ 。

lcm=29222879530390785742605477742453420902991175027283185502224574005903986263169096240656898659768251131170153243355896585116206546809026765977240398343841844413932022486239027317290376878970267549705130293352356070399197681533774641809920245792277386418338948725614463605422608450981946445029718369662946357705499281823362508397007696635982211082237545037851621498721235291885337720080893169582699780294708804334786758878624750037193583886404728146815380945201540
n=2228582814888322539771891137733971181257097900700884269780928959802985615275288341111620316685788511492461651695428697100554113037555468881895905318207963274537589532345166133820089694201148988443496514751074857966136041157336680322417272183777409351597268908625677512781049274972325769500959755298004643407023188886359792411648183582888979219785653927285023667015990929441992061367448365123092899330885934801013411132173550954938961520075931155848843991824723727187297663420031211934554344568933171179175237722716971390081142435747796272698118097337803559316319210494963021258386613285360239662354953552369582646607
c=2201106853018581355094419701171997731036843750081916703504266002782698731288317690546242336345890702261049147276084047271293227314969153138029180802403349980519050857699472720333400348342466190619778247784674359271736569275019018808569614566880813745619585529292155639979431043005511905548345767685472340763230813956617014122768477272236518467064016133244646900977041959848793579834848773548018337874928875046550721154575652528641850315494384644468806058021812603748441246192757443085386516155814337307681275922473564325028703523754319072117202083218199961250157611091952832038366393322275194833927035639232266868638
e = 65537

import gmpy2

d=gmpy2.invert(e,lcm)
m=pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))

warm_up

代码粗糙的质感刺痛了我的眼睛，我似乎能通过这文件锋利的边缘窥探到“它”的本质，但是我不能这样做，我害怕我会看到这道题背后卑劣歹毒如同幽灵一般的隐喻。

Hint: 是一个由RSA衍生出来的密码系统，还挺年轻的。

from Crypto.Util.number import getPrime as getprime ,long_to_bytes,bytes_to_long,inverse
from vanish import flag
from sympy import isprime,nextprime
import random

m=bytes_to_long(flag)
p=getprime(512)
q=nextprime(512)
n=p*q

r=random.randint(1,n)
g=random.randint(1,n)

c=(pow(g,m,n*n)*pow(r,n,n*n))%(n*n)

print "c=%d"%(c)
print "n=%d"%(n)
print "g=%d"%(g)

'''
c=14643617840485727260687883789514337554960495078025159182484344940901600090810578182116617501128323641882943106663241094886209190199404002314247096613925999812837877843566116787148411743428714726661042213165729562285577768043368385746666607442372252641495230532588344276427261824205414379772728577442269620217619275
n=5650215343715484415924649393302012617620686312875699289646188186788806118580423414401283971780836312947326343790326120926819026727018136169739576760024802083
g=786539430846729749998127835613552594423101498023741082894370020014675937062722533682541592019332908209917194089077366019472368764411032602494945304850258108

'''

1999年提出的Paillier同态加密，这里为一般情况，参考算法代入计算即可。

c=14643617840485727260687883789514337554960495078025159182484344940901600090810578182116617501128323641882943106663241094886209190199404002314247096613925999812837877843566116787148411743428714726661042213165729562285577768043368385746666607442372252641495230532588344276427261824205414379772728577442269620217619275
n=5650215343715484415924649393302012617620686312875699289646188186788806118580423414401283971780836312947326343790326120926819026727018136169739576760024802083
g=786539430846729749998127835613552594423101498023741082894370020014675937062722533682541592019332908209917194089077366019472368764411032602494945304850258108

import gmpy2

def L(x):
	return (x-1)//n

#分解n
p=521
q=10844943078148722487379365438199640340922622481527253914867923583087919613398125555472713957352852807960319277908495433640727498516349589577235272092178123
lcm=gmpy2.lcm(p-1,q-1)
u=gmpy2.invert(L(pow(g,lcm,n*n)),n)

m=L(pow(c,lcm,n*n))*u%n
print(bytes.fromhex(hex(m)[2:]))

ezrsa

或许是出于理性亦或是恐惧，总之我把这道题藏了起来。我暗中感觉到它有着诱人发狂的能力，我不能让更多人见到它，这道题是黑暗中不可名状的恶兽。

from Crypto.Util.number import *
from secret import e3,hint,flag


e1=2
p1=1407082287125181464014767936705655200254016298201118080211963
q1=4483497795612950594917254979514794222210515250120330465584919
hint=int(hint.encode('hex'),16)
c1=pow(hint,e1,p1*q1)

e2=5
q2=898033
p2=1027487
assert e3<=300
c2=pow(e3,e2,p2*q2)


q3=16471885912035642894544190467774867069446937372970845578732298073
p3=21122913513992623721920275602985463699928507831138027
#flag='flag{*************}'
flag=int(flag.encode('hex'),16) 
c3=pow(flag,e3,p3*q3)

print c1 #1094524901124574666920734011106836493645715846893412590792284228545024220996290692759698315651894211650519689592667719756

print c2 #779811265199

print c3 #346925245648012783854132941104554194717281878370806475831055718275298366664505658836564073456294047402009856656647760

RSA小套娃题。

先从 $e1,p1,q1,c1$ 解hint，$e=2$ 的情形为Rabin加密

import gmpy2

def rabin_decrypt(c, p, q, e=2):
	n = p * q
	mp = pow(c, (p + 1) // 4, p)
	mq = pow(c, (q + 1) // 4, q)
	yp = gmpy2.invert(p, q)
	yq = gmpy2.invert(q, p)
	r = (yp * p * mq + yq * q * mp) % n
	rr = n - r
	s = (yp * p * mq - yq * q * mp) % n
	ss = n - s
	return (r, rr, s, ss)
	
e1=2
p1=1407082287125181464014767936705655200254016298201118080211963
q1=4483497795612950594917254979514794222210515250120330465584919
c1=1094524901124574666920734011106836493645715846893412590792284228545024220996290692759698315651894211650519689592667719756
m=rabin_decrypt(c1,p1,q1,e1)

for k in m:
	try:
		print(bytes.fromhex(hex(k)[2:]))
	except:
		pass
    
#hint: https://eprint.iacr.org/2013/117.pdf

四解中有一解为真正的hint，得到一个paper网址：https://eprint.iacr.org/2013/117.pdf

再从 $e2,p2,q2,c2$ 解 $e3$，常规RSA

p2=1027487
q2=898033
e2=5
c2=779811265199

import gmpy2

fn2=(p2-1)*(q2-1)
d2=gmpy2.invert(e2,fn2)
e3=pow(c2,d2,p2*q2)
print(e3)

#e3=239

最后从 $e3,p3,q3,c3$ 解 $m$，难点在于存在情形 $e \mid p-1,e \mid q-1$，参考hint论文，在有限域下求 $e$ 次根

###Sage
c = 346925245648012783854132941104554194717281878370806475831055718275298366664505658836564073456294047402009856656647760
p = 21122913513992623721920275602985463699928507831138027
q = 16471885912035642894544190467774867069446937372970845578732298073
e = 239

P.<a>=PolynomialRing(Zmod(p),implementation='NTL')
f=a^e-c
mps=f.monic().roots()

P.<a>=PolynomialRing(Zmod(q),implementation='NTL')
g=a^e-c
mqs=g.monic().roots()

for mpp in mps:
    x=mpp[0]
    for mqq in mqs:
        y=mqq[0]
        solution = hex(CRT_list([int(x), int(y)], [p, q]))[2:]
        if solution.startswith('666c'):
            print(solution)

REVERSE

⎛⎝WDNMD⎠⎞

我起了，一枪秒了，有什么好说的（白给签到题）

F5未发现有用信息，回到汇编代码，发现main()函数里有flag后半段：

回到全局反汇编窗口，Alt+T全局搜索”flag{“，发现data段藏着flag前半段：

98年的，我玩不过她

如果不是真的喜欢，谁又愿意做舔狗呢

从字符串窗口定位入口在sub_140011950函数：

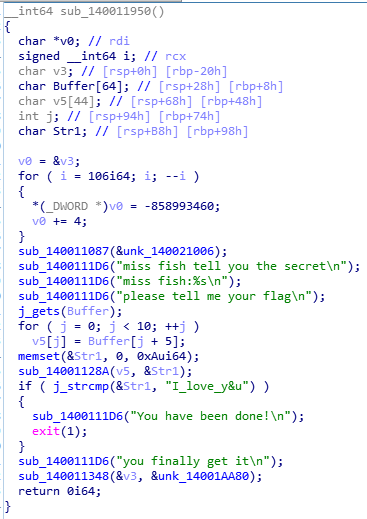
获取长度为10的字符串存入Buffer数组，令v5[0:10]=Buffer[5:15]，经sub_14001128A函数处理后得到Str1，将其与 I_love_y&u 比较，相等则正确。

跟进sub_14001128A函数，发现switch-case遍历结构：

分别把switch-case结构中case各字符对应的结果字符求出，逐个比对 I_love_y&u 每个字符，还原得原始Buffer[5:15]值，添加前四个字符“flag{”可得flag。

four steps

做re好像挺简单的，不就是解决了这四个步骤不就好了。

从字符串窗口定位入口在sub_1400159A0函数：

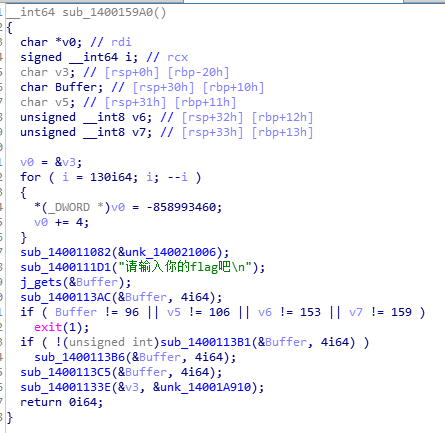
读字符串存入Buffer，第一步sub_1400113AC函数处理，比对Buffer[0:4]；第二步sub_1400113B1函数处理Buffer[4:8]；第二步返回值为0则进入第三步，sub_1400113B6函数处理Buffer[8:12]；第四步sub_1400113C5函数处理Buffer[12:16]。

第一步

先初始化256大小的数组a，再做奇数下标的值前后交换，爆破Buffer[0:4]：

a=[j for j in range(256)]
for j in range(128):
	if j%2==1:
		a[j],a[256-j]=a[256-j],a[j]

c=[96,106,153,159]
m=''
for cc in c:
	for k in range(128):
		if a[k]^6==cc:
			m+=chr(k)
			break
print(m)
#flag

第二步

根据等式爆破，选择合适结果：

m=''

for x4 in range(128):
	for x5 in range(128):
		for x6 in range(128):
			for x7 in range(128):
				if (x5>>4)+(x4>>4)==13 and (x7>>4)+(x6>>4)==13 and (x4&0xF)-(x5&0xF)==10 and (x6&0xF)-(x7&0xF)==11 and (x6&0xF)-(x5&0xF)==13 and (x5>>4)==(x6>>4):
					m=chr(x4)+chr(x5)+chr(x6)+chr(x7)
					print(m)
#6个结果，选择正确的
#{ans

第三步
变了码表的base64编码，码表为AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpQqRrSsTtUuVvWwXxYyZz1234567890+/，编码结果o3kZl3==，使用工具解码得wer_。

第四步

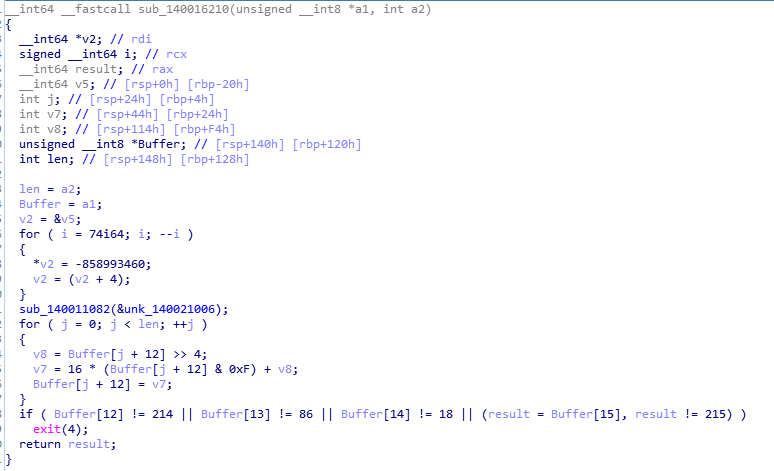
同第一步，爆破Buffer[12:16]：

c=[214,86,18,215]
m=''
for cc in c:
	for k in range(128):
		if 16*(k&0xF)+(k>>4)==cc:
			m+=chr(k)
			break
print(m)
#me!}

拼接四步得到的字符串得flag。

Lazzaro

CTF弱鸡自进阶

CBCTF 第三届赛博杯

Misc

α层

guess

Web

尖尖的商店

Hacked_By_V

Crypto

check_in

warm_up

ezrsa

REVERSE

⎛⎝WDNMD⎠⎞

98年的，我玩不过她

four steps

CBCTF 第三届赛博杯

Misc

sign_in

α层

guess

Web

尖尖的商店

Hacked_By_V

Crypto

check_in

warm_up

ezrsa

REVERSE

⎛⎝WDNMD⎠⎞

98年的，我玩不过她

four steps