数字中国是十九大提出的新时代国家信息化发展的新战略。2021数字中国创新大赛,作为数字中国建设峰会“一会、一展、一赛”的重要组成部分, 将继续采取多赛道并行的竞赛形式,设置数字党建、数字政府、大数据、智慧医疗、鲲鹏计算、网络安全、集成电路设计、青少年AI机器人八个赛道,紧贴数字中国建设峰会主题,围绕核心前沿技术与信息技术应用创新设置赛题,以多维度立体化的角度诠释“数字中国”。
第二届“虎符网络安全赛道“将在去年首次将PK体系与传统网络安全竞赛相结合的优势基础上,继续保持Wintel+PK双体系并行模式进行比赛,以“PK体系”在网络安全赛事中的创新升级应用作为赛事的核心驱动。同时在此基础上进行包括赛事场景、评委阵容以及选手权益在内的三大升级。
https://www.ichunqiu.com/2021hfctf
rank: 80+
Misc
你会日志分析吗
线索只有一份access.log,你能从中分析到什么?
明显能看出access.log日志文件中包含SQL时间盲注的记录,直接拉到最后看
?id=1'%20and%20if(ord(substr((select%20flag%20from%20flllag),xx,1))=xx,sleep(2),1)语句,
逐个字符猜解,正确情形会延迟2s,观察每行前一列的时间秒数,不连续的部分前一个字符即为正确字符。
懒写脚本,逐个手撸得到一串十进制数
90 109 120 104 90 51 116 90 98 51 86 102 89 88 74 108 88 51 78 118 88 50 100 121 90 87 70 48 102 81 61 61,
转为字符为base64编码字符串ZmxhZ3tZb3VfYXJlX3NvX2dyZWF0fQ==,解码即为flag。
flag
flag{You_are_so_great}
Crypto
cubic
Please give me 6 pairs of positive integers (x,y,z) satisfying the equation
x/(y+z) + y/(z+x) + z/(x+y) = 6
给出著名不定方程 $\cfrac{x}{y+z}+\cfrac{y}{x+z}+\cfrac{z}{x+y}=6$ 的6组正整数解,乍看容易实则不然。
方程在整数范围内易通过爆破求得多解,而正整数范围内很难用初等代数人工求得多解,需结合抽象代数解决。
背景参考:史上最贱的数学题
把 $x,y,z$ 看为 $a,b,c$,展开化简为:
$a^3+b^3+c^3-5(a^2b+ab^2+a^2c+ac^2+b^2c+bc^2)-9abc=0$
结合引用论文 An unusual cubic representation problem,将方程映射到二维空间,即 $(a,b,c) \rightarrow (x,y)$。
$(a,b,c) \rightarrow (x,y)$ 映射关系式:
$\begin{cases} x=\cfrac{-4(a+b+2c)(N+3)}{(2a+2b-c)+(a+b)N}=\cfrac{-36(a+b+2c)}{8a+8b-c} \\ y=\cfrac{4(a-b)(N+3)(2N+5)}{(2a+2b-c)+(a+b)N}=\cfrac{612(a-b)}{8a+8b-c} \end{cases}$
取 $(a,b,c)=(1,-1,0)$,得到椭圆曲线的Weierstrass形式方程:
$E_6:y^2=x^3+(4N^2+12N-3)x^2+32(N+3)x=x^3+213x^2+288x$
在曲线上易取出基点 $G$ 作为初始点,根据不定方程的 $(ka,kb,kc)$ 通解特性,可分别将基点 $G$ 数乘得到 $2G,3G,\cdots$,再分别通过关系式映射回 $(a,b,c)$,以条件判断 $a>0,b>0,c>0$,得到的 $(a,b,c)$ 即为不定方程的正整数解。
$(x,y) \rightarrow (a,b,c)$ 映射关系式:
$\begin{cases} \cfrac{a}{a+b+c}=\cfrac{8(N+3)-x+y}{2(4-x)(N+3)} \\ \cfrac{b}{a+b+c}=\cfrac{8(N+3)-x-y}{2(4-x)(N+3)} \\ \cfrac{c}{a+b+c}=\cfrac{-4(N+3)-(N+2)x}{(4-x)(N+3)} \end{cases}$
脚本:
1 | #Sage |
再通过pwntools与环境交互得flag。
1 | from pwn import * |
flag
flag{1f88de74-b6af-4b2b-abd5-46356151698b}
Reverse
redemption_code
所谓的虐心手游,连发的兑换码都这么复杂。
反编译看main()函数,输入字符串key分别经过两次处理:
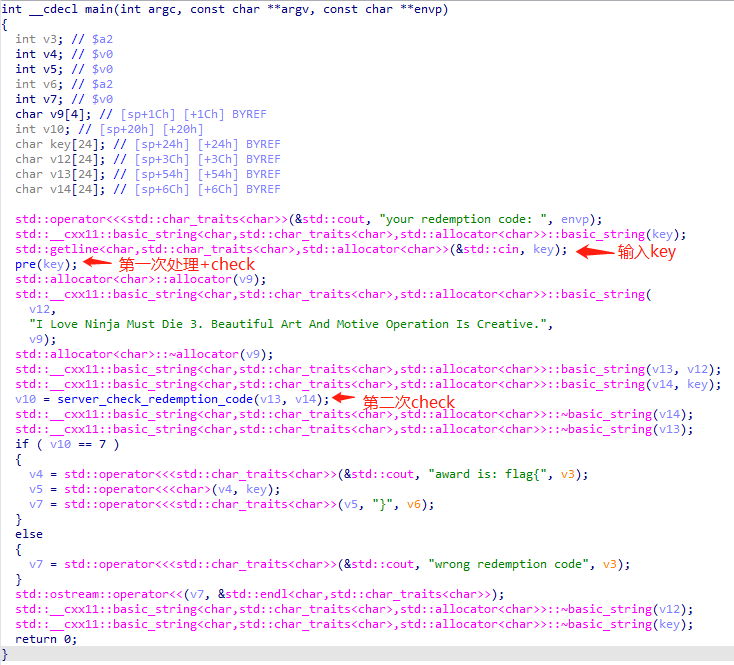
第一层处理,pre()函数:
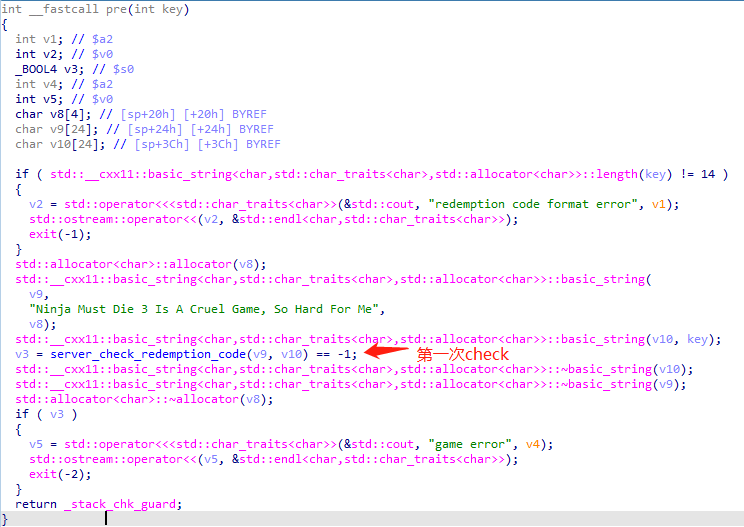
先判断输入key长度len(key)==14,再与字符串ss1="Ninja Must Die 3 Is A Cruel Game, So Hard For Me"共同作为server_check_redemption_code()函数参数:
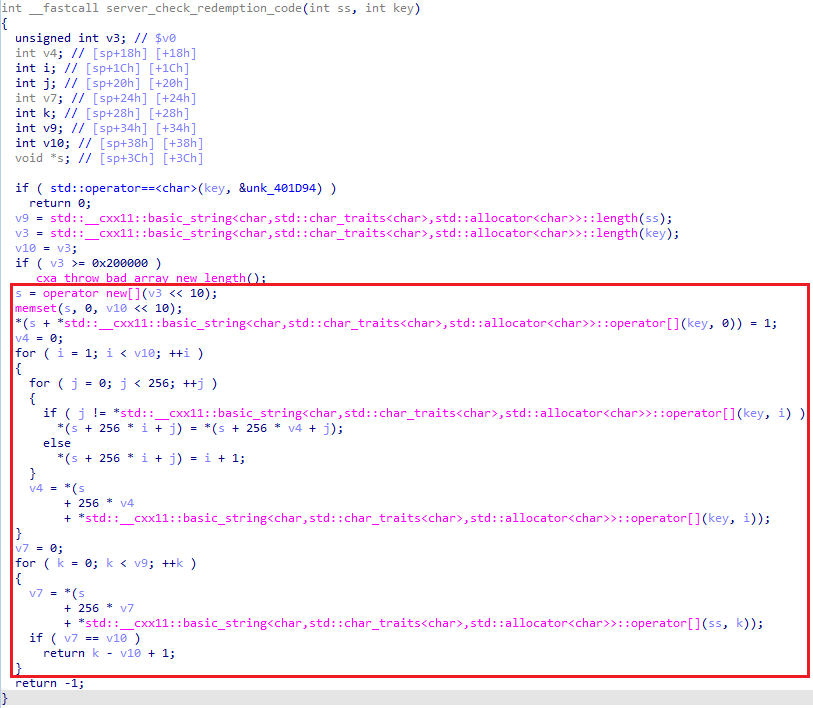
server_check_redemption_code()函数的核心部分,通过编写代码测试,功能为返回key中符合字符串ss子串的最大长度,s数组保存逐行判断得到的连续字符状态值,如整个key为ss子串,返回起始下标值k-len(key)+1,否则返回-1。
第二层处理,判断输入key长度len(key)==14,再与字符串ss2="I Love Ninja Must Die 3. Beautiful Art And Motive Operation Is Creative."共同作为server_check_redemption_code()函数参数。
第一次check,需返回值不等于-1进到第二次check,第二次check需返回值为7输出flag,即key既是ss1子串,又是ss2从下标7开始的子串,即共有子串Ninja Must Die。
flag
flag{Ninja Must Die}
Web
签到
师傅们常说,要善于学习,细致入微;师傅们也常说,要善于分享,总结归纳。
hint: 2021年3月28日,PHP维护的官方Git服务器 git.php.net 被袭击,其Git仓库遭到恶意篡改。如果开发者使用这些遭到篡改的源代码进行网页的开发的话,网站就会在不知情的情况下被感染。
开始在环境里翻了一圈无头绪,放hint后查找此事件才知道这是几天前的事,紧跟时事的出题人。
来龙去脉:
3月28日,攻击者使用PHP的作者Rasmus Lerdorf和Jetbrains开发者Nikita Popov的账号,向git.php.net服务器上的 php-src 存储库推送了两次恶意提交。
经观察,在两个恶意提交中,攻击者在上游发布了一个假装成修正文字输入错误的神秘修改。
攻击者以Rasmus Lerdorf的身份签署的恶意提交(非法)植入远程代码执行后门。
仔细检查一下新增的第370行调用
zend_eval_string函数的地方,可以发现,这段代码实际上是为运行被劫持的PHP版本的网站植入了一个后门,以获得轻松的远程代码执行(RCE)。PHP的开发者表示,如果字符串以
zerodium开头,这一行就会从User-AgenttHTTP头内执行PHP代码。此外,恶意代码中包含了一条注解 “REMOVETHIS: sold to zerodium, mid 2017”。值得注意的是,Zerodium是一家知名的零日漏洞经纪商,而注释的意思是“漏洞在2017年中出售给了zerodium”。对此,Zerodium的CEO Chaouki Bekrar认为攻击者很可能试图出售这个漏洞,但找不到卖家,所以攻击者干脆自己恶搞。
同时参考Linkedin上的一文:Official PHP Git server attacked,照样构造payload,开始没注意到属性是User-Agentt而不是默认的User-Agent,百试不出…
payload(加在HTTP头)
列目录:User-Agentt: zerodiumsystem('ls /');
读文件:User-Agentt: zerodiumsystem('cat /flag');
flag
flag{cc5dbc99-fd75-41f8-87f6-825c7e08f016}