后量子密码学(Post-Quantum Cryptography,PQC),又称抗量子计算密码学,是密码学的一个研究领域,专门研究能够抵抗量子计算机的加密算法,特别是公钥加密(非对称加密)算法。不同于量子密码学,后量子密码学使用现有的电子计算机,不依靠量子力学,它依靠的是密码学家认为无法被量子计算机有效解决的计算难题。
在公钥加密方面,后量子密码学的研究方向包括了格密码学(Lattice-based Cryptography)、容错学习问题(LWE)、多变量密码学(英语:Multivariate Cryptography)、散列密码学(英语:Hash-based Cryptography)、编码密码学(Code-based Cryptography)与超奇异椭圆曲线同源密码学(Supersingular Isogeny Key Exchange)。密码学家认为,基于这些计算难题有望构建出不受量子计算机的威胁的公钥加密系统,替代现有的方案。
基本概念
超奇异椭圆曲线
若曲线 $E$ 定义在有限域 $F_{p^r} (r \in \Z^*)$ 下,若 $E$ 的阶 $\text{order}$ 满足 $\text{order} = 1 \pmod p$,则$E$ 是一条超奇异椭圆曲线 (Supersigular Elliptic Curve)。
1 | p = 2^4*3^3-1 |
j不变量(j-invariant)
对于椭圆曲线来说,j不变量可以简单理解为一个判定两条椭圆曲线是否同构的值。也就是说,任何一个曲线都有自己独特的j不变量,而如果两条曲线的j不变量相等,则说明这两条曲线彼此同构。而由于同构的曲线本质上都可以看作同一条曲线,这也就说明,一个j不变量其实在同构意义上其实就唯一对应着一条曲线。
j不变量相同意味着,可以找到一个同构,将一条曲线映射到另一条曲线上。
二次扩域 $F_{p^2}$ 下共有 $p^2$ 个j不变量。
1 | p = 2^4*3^3-1 |
同源(isogeny)
一个可分的(separable)同源可以描述为:对于一条曲线 $E$ 以及 $E$ 上一个子群 $G$,都可以构造一个以 $G$ 为核的映射 $\phi: E \rightarrow E’$,这个映射就是同源,映射到的曲线 $E’$ 就叫做这个同源的陪域(codomain)。
可以用这个子群 $G$ 和曲线 $E$ 生成一个同源,映射到的曲线 $E’$ 不再是原来的曲线E了,它的j不变量发生了变化。可以用如下方式求出曲线上所有阶为2的点:
1 | torsion_2_points = E(0).division_points(2) |
同源图
二次扩域 $F_{p^2}$ 下所有超奇异椭圆曲线的j不变量的图,对所有点的 $n$-torsion都画出这些边,就得到了完整的 $n$-isogeny 的同源图,能表示出这个二次扩域中所有度为 $n$ 的 isogeny 的映射关系。
之所以边是无向的,就是因为有对偶映射,如果 $E$ 向 $E’$ 有个度为 $n$ 的同源,那么 $E’$ 向 $E$ 也一定有一个度为 $n$ 的对偶同源。
模多项式(modular polynomial)
用一个多项式关联了 $d$-isogeny 中互为邻居的两个j不变量。如果知道了一个j不变量,那么可以将其代入对应度的modular polynomial去求根,得到的所有根就是所有作为他的邻居的j不变量。
modular polynomial对应的度较低的多项式形式参考:Modular polynomials (mit.edu)
参考:
超奇异同源密钥交换(SIDH)
超奇异椭圆曲线同源密码学(Supersingular Elliptic Curve Isogeny Cryptography)是利用超奇异椭圆曲线(Supersingular Elliptic Curves)与超奇异同源图(Supersingular Isogeny Graphs)的数学性质的密码学,可以实现超奇异同源密钥交换(Supersingular Isogeny Key Exchange,SIKE)(协议为超奇异同源Diffie-Hellman密钥交换协议,SIDH),具有前向安全性。其使用方法和现有的Diffie-Hellman密钥交换相似,有望直接替代当前的常规椭圆曲线密钥交换(ECDH)。
Diffie-Hellman基本协议:
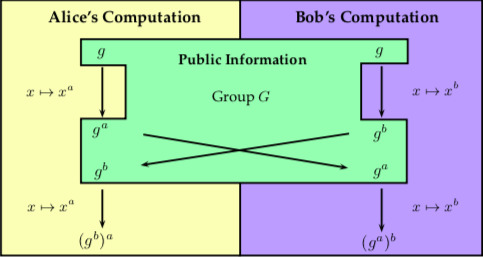
抽象Diffie-Hellman:
Alice的秘密是 $a$,她的计算先做→,得到 $g^a$,再做↓,得到 $g^{ab}$。而Bob的秘密是 $b$,他先做↓,再做→。殊途同归得到 $g^{ab}$。
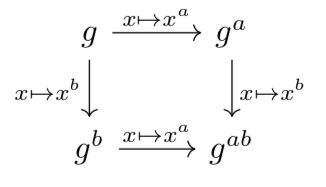
SIDH构造的简化版本
SIDH的基本代数结构是超奇异椭圆曲线群 $E$ 和超奇异同源(Isogeny)$\phi$。基本思路如下图所示:
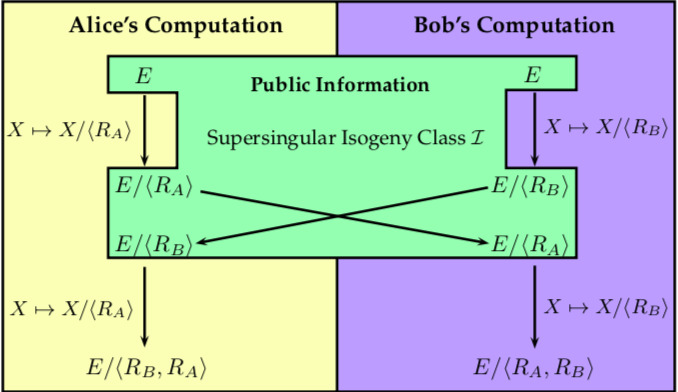
首先,超奇异椭圆曲线群 $E$ 理解为一个群。其次,构造用到的超奇异同源 $\phi : E \mapsto E’$ 是从群 $E$ 到群 $E’$ 的一种群同态。算法类似DH算法分为以下两个步骤:
- 首先,Alice选取一个点 $R_A \in E$,$\langle R_A \rangle$ 确定了群 $E$ 的一个子群,然后可以计算得到一个从 $E$ 映射到其子群 $E_A$ 的同源 $\phi_A: E \mapsto E_A$,这是Alice的秘密信息。Alice发送公开信息 $E_A$ 给Bob。
- 同样,Bob选择点 $R_B\in E$,然后计算得到 $\phi_B: E \mapsto E_B$,把公开信息 $E_B$ 发送给Alice。
最终Alice算出 $E/\langle R_B, R_A \rangle$,Bob算出 $E/\langle R_A, R_B \rangle$。上图中的 $E/\langle R_A \rangle$ 和 $E/\langle R_B \rangle$ 分别是 $E_A$ 和 $E_B$,这样表达是为了与之前的表达一致,其实这里并不是做商群,而是表达说 $\phi_A$ 的Kernel是 $\langle R_A \rangle$。目前的科技文献大多使用这种表达。
上面说到,$E_A$ 是曲线群 $E$ 的子群,它由同源 $\phi_A$ 决定,可理解为群同态 $\phi_A$ 映射到 $E$ 上的像 (Image)形成的子群。同理,$E_{BA}$ 是同源 $\phi_{BA}$ 映射到 $E$ 上的子群,而同源 $\phi_{BA}$ 是由 $\langle R_B, R_A \rangle$ 决定的,即同源 $\phi_{BA}$ 的Kernel是 $\langle R_B, R_A \rangle$。
SIDH构造的细化版本
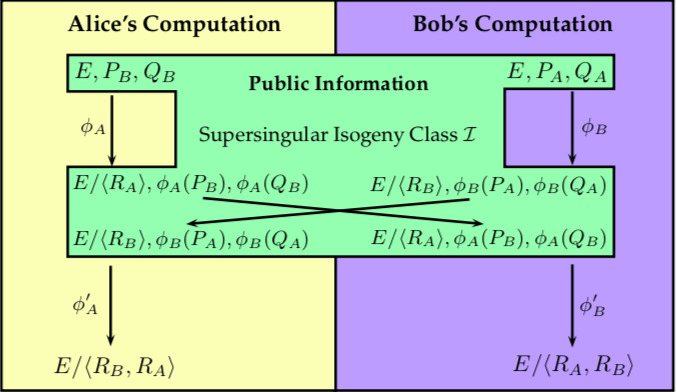
为了满足Alice在没有Bob的秘密信息的情况下能计算出 $E_{BA}$ 的要求,SIDH需要使用更多的参数设计和相关计算。算法增加描述如下:
SIDH参数设计
首先,选择超奇异椭圆曲线 $E$ 作为公开参数。然后Alice随机选择两个元素 $P_A, Q_A \in E$,并公开作为自己的公共参数。同样,Bob也随机选择两个元素 $P_B, Q_B \in E$ 并公开。
Alice的操作
- 随机选择两个整数 $s_A$ 和 $t_A$ 作为秘密信息,计算 $R_A = s_A P_A + t_A Q_A\in E$,并由 $R_A$ 计算得到一个从 $E$ 映射到其子群 $E_A$ 的同源 $\phi_A: E \mapsto E_A$,这也是Alice的秘密信息;
- 获取Bob的公开信息,并计算 $\phi_A(P_B)$ 和 $\phi_A(Q_B)$,这些是公开信息;
- Alice发送公开信息 $E_A$、$\phi_A(P_B)$ 和 $\phi_A(Q_B)$ 给Bob。
Bob的操作
- 随机选择两个整数 $s_B$ 和 $t_B$ 作为秘密信息,计算 $R_B = s_B P_B + t_B Q_B\in E$,并由 $R_B$ 计算得到一个从 $E$ 映射到其子群 $E_B$ 的同源 $\phi_B: E \mapsto E_B$,这也是Bob的秘密信息;
- 获取Alice的公开信息,并计算 $\phi_B(P_A)$ 和 $\phi_B(Q_A)$,这些是公开信息;
- Bob发送公开信息 $E_B$、$\phi_B(P_A)$ 和 $\phi_B(Q_A)$ 给Alice。
秘密值的计算
Alice计算子群 $E_{BA}$ ,方法如下:
- 注意,此时Alice掌握的信息是 $s_A$、$t_A$、$R_A$、$\phi_B(P_A)$ 和 $\phi_B(Q_A)$,她想计算得到 $\phi_B(R_A)$。并且要强调,$\phi_B$ 是一种群同态。
- 利用群同态的属性可计算得到:$\phi_B(R_A) = \phi_B(s_A P_A + t_A Q_A) = s_A \phi_B(P_A) + t_A \phi_B(Q_A)$ 。
- 根据 $\phi_B(R_A)$ 计算 $E_{BA}$。$E_{BA}$是曲线群 $E$ 的子群,是以 $\phi_B (R_A)$ 为Kernel的群同态映射到 $E$ 上的子群。这个群同态也就是Isogeny,这个Isogeny记为 $\phi_{BA}$ 。
类似的,Bob可以计算子群 $E_{AB}$:
- $\phi_A(R_B) = s_B \phi_A(P_B) + t_B \phi_A(Q_B)$;
- 由此可计算得 $E_{AB}$ ;
最后冲顶的一步,计算秘密值。首先要明确,很可能 $E_{BA} \ne E_{AB}$,但是,$E_{BA}$ 同构于 $E_{AB}$。利用同构曲线的一个属性:所有同构曲线的J-Invariant值相同。于是Alice和Bob分别计算这两条曲线的J-Invariant值 $J(E_{BA})$ 和 $J(E_{AB})$,这就是他们共同拥有的秘密。J-Invariant的计算定义可在标准教科书中找到,本文把它视为黑盒子使用。
Sage代码
参数设置
1 | #选取一条在素域k上的超奇异椭圆曲线 |
Alice 的操作
1 | #Alice选择两个随机数并计算自己的秘密值RA |
Bob 的操作
1 | #Bob的工作类似 |
秘密值计算
1 | # Alice计算秘密值 |
Castryck-Decru攻击
(待补充)
参考:

