块密码/分组密码
在密码学中,分组加密(英语:Block cipher),又称分块加密或块密码,是一种对称密钥算法。它将明文分成多个等长的模块(block),使用确定的算法和对称密钥对每组分别加密解密。分组加密是极其重要的加密协议组成,其中典型的如AES和3DES作为美国政府核定的标准加密算法,应用领域从电子邮件加密到银行交易转帐,非常广泛。
分组加密包含两个成对的算法:加密算法 $E$ 和解密算法 $D$,两者互为反函数。每个算法有两个输入:长度为 $n$ 位的组,和长度为 $k$ 位的密钥;两组输入均生成 $n$ 位输出。将两个算法看作函数,$K$ 表示长度为 $k$ 的密钥(密钥长度),$P$ 表示长度为 $n$ 的分组,$P$ 也被表示为明文,$C$ 表示密文,则满足:
$E_K(P) = C \; ; \quad E_K^{-1}(C)=P$
$E_K(P) := E(K,P): \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n,$
对于任意密钥 $K$,$E_K(P)$ 是输入的组的一个置换函数,且可逆地落在 $\{0,1\}^n$ 区间。$E$ 的反函数(解密算法)定义为:
$E_K^{-1}(C) := D_K(C) = D(K,C): \{0,1\}^k \times \{0,1\}^n \rightarrow \{0,1\}^n,$
例如,一个分组加密算法使用一段 128 位的分组作为明文,相应输出 128 位的密文;而其转换则受加密算法中第二个输入的控制,也就是密钥 $k$。解密算法类似,使用 128 位的密文和对应的密钥,得到原 128 位的明文。
每一个密钥实际上是选择了 $n$ 位输入排列的 $(2^n)!$ 种组合中的一种。
大多数的分组密码在在加密算法中会重复使用某一函数进行多轮运算,典型的轮数在4-32次之间,每一轮的函数R使用不同的子密钥 $K_i$,由原密钥生成,作为输入:
$M_i = R_{K_i}(M_{i-1})$
其中 $M_{0}$ 是最初的明文,$M_{i}$ 是第 $i$ 轮加密后的密文。
AES
高级加密标准(英语:Advanced Encryption Standard,缩写:AES),又称Rijndael加密法,是美国联邦政府采用的一种区块加密标准。这个标准用来替代原先的DES,已经被多方分析且广为全世界所使用。经过五年的甄选流程,高级加密标准由美国国家标准与技术研究院(NIST)于2001年11月26日发布于FIPS PUB 197,并在2002年5月26日成为有效的标准。现在,高级加密标准已然成为对称密钥加密中最流行的算法之一。
该算法为比利时密码学家Joan Daemen和Vincent Rijmen所设计,结合两位作者的名字,以Rijndael为名投稿高级加密标准的甄选流程。
加密方法
严格地说,AES和Rijndael加密法并不完全一样(虽然在实际应用中两者可以互换),因为Rijndael加密法可以支持更大范围的区块和密钥长度:AES的区块长度固定为128比特,密钥长度则可以是128,192或256比特;而Rijndael使用的密钥和区块长度均可以是128,192或256比特。加密过程中使用的密钥是由Rijndael密钥生成方案产生。
大多数AES计算是在一个特别的有限域完成的。
AES加密过程是在一个4×4的字节矩阵上运作,这个矩阵又称为“体(state)”,其初值就是一个明文区块(矩阵中一个元素大小就是明文区块中的一个Byte)。(Rijndael加密法因支持更大的区块,其矩阵的“列数(Row number)”可视情况增加)加密时,各轮AES加密循环(除最后一轮外)均包含4个步骤:
- AddRoundKey 矩阵中的每一个字节都与该次回合密钥(round key)做XOR运算;每个子密钥由密钥生成方案产生。
- SubBytes 透过一个非线性的替换函数,用查找表的方式把每个字节替换成对应的字节。
- ShiftRows 将矩阵中的每个横列进行循环式移位。
- MixColumns 为了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每内联的四个字节。最后一个加密循环中省略MixColumns步骤,而以另一个AddRoundKey取代。
1 | //Java实现 |
DES
数据加密标准(英语:Data Encryption Standard,缩写为 DES)是一种对称密钥加密块密码算法,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上广泛流传开来。它基于使用56位密钥的对称算法。这个算法因为包含一些机密设计元素,相对短的密钥长度以及怀疑内含美国国家安全局(NSA)的后门而在开始时有争议,DES因此受到了强烈的学院派式的审查,并以此推动了现代的块密码及其密码分析的发展。
DES现在已经不是一种安全的加密方法,主要因为它使用的56位密钥过短。
加密方法
DES是一种典型的块密码—一种将固定长度的明文通过一系列复杂的操作变成同样长度的密文的算法。对DES而言,块长度为64位。同时,DES使用密钥来自定义变换过程,因此算法认为只有持有加密所用的密钥的用户才能解密密文。密钥表面上是64位的,然而只有其中的56位被实际用于算法,其余8位可以被用于奇偶校验,并在算法中被丢弃。因此,DES的有效密钥长度仅为56位。
算法的整体结有16个相同的处理过程,称为“回次”(round),并在首尾各有一次置换,称为IP与FP(或称IP-1,FP为IP的反函数(即IP“撤销”FP的操作,反之亦然)。IP和FP几乎没有密码学上的重要性,为了在1970年代中期的硬件上简化输入输出数据库的过程而被显式的包括在标准中。
在主处理回次前,数据块被分成两个32位的半块,并被分别处理;这种交叉的方式被称为费斯妥结构。费斯妥结构保证了加密和解密过程足够相似—唯一的区别在于子密钥在解密时是以反向的顺序应用的,而剩余部分均相同。这样的设计大大简化了算法的实现,尤其是硬件实现,因为没有区分加密和解密算法的需要。
费斯妥函数(F函数)将数据半块与某个子密钥进行处理。然后,一个F函数的输出与另一个半块异或之后,再与原本的半块组合并交换顺序,进入下一个回次的处理。在最后一个回次完成时,两个半块需要交换顺序,这是费斯妥结构的一个特点,以保证加解密的过程相似。
费斯妥函数(F函数)每次对半块(32位)进行操作,并包括四个步骤:
- 扩张 用扩张置换将32位的半块扩展到48位,其输出包括8个6位的块,每块包含4位对应的输入位,加上两个邻接的块中紧邻的位。
- 与密钥混合 用异或操作将扩张的结果和一个子密钥进行混合。16个48位的子密钥—每个用于一个回次的F变换—是利用密钥调度从主密钥生成的。
- S盒 在与子密钥混合之后,块被分成8个6位的块,然后使用“S盒”,或称“置换盒”进行处理。8个S盒的每一个都使用以查找表方式提供的非线性的变换将它的6个输入位变成4个输出位。S盒提供了DES的核心安全性—如果没有S盒,密码会是线性的,很容易破解。
- 置换 最后,S盒的32个输出位利用固定的置换,“P置换”进行重组。这个设计是为了将每个S盒的4位输出在下一回次的扩张后,使用4个不同的S盒进行处理。
S盒,P置换和E扩张各自满足了克劳德·香农在1940年代提出的实用密码所需的必要条件,“混淆与扩散”。
弱密钥
在DES的计算中,56bit的密钥最终会被处理为16个轮密钥,每一个轮密钥用于16轮计算中的一轮,DES弱密钥会使这16个轮密钥完全一致,所以称为弱密钥。
四个弱密钥:
1 | \x01\x01\x01\x01\x01\x01\x01\x01 |
如果不考虑校验位的密钥,以下也属于弱密钥:
1 | \x00\x00\x00\x00\x00\x00\x00\x00 |
如果使用弱密钥,PC1计算的结果会导致轮密钥全部为0、全部为1或全部01交替。
因为所有的轮密钥都是一样的,并且DES是 Feistel网络的结构,这就导致加密函数是自反相 (self-inverting) 的,结果就是加密一次看起来没什么问题,但是如果再加密一次就得到了明文。
部分弱密钥
部分弱密钥是指只会在计算过程中产生两个不同的子密钥,每一个在加密的过程中使用8次。这就意味着这对密钥$k_1$ 和 $k_2$ 有如下性质:$E_{k_1}(E_{k_2}(M))=M$。
6个常见的部分弱密钥对:
1 | 0x011F011F010E010E + 0x1F011F010E010E01 |
加解密工具
openssl
加密:
openssl enc -aes-128-cbc -in plain.txt -out encrypt.txt -iv f123 -K 1223 -p-p: 打印加密用的salt,key,iv
解密:
openssl aes-128-cbc -d -in encrypt.txt -out encrypt_decrypt.txt -S E0DEB1EAFE7F0000 -iv F1230000000000000000000000000000 -K 12230000000000000000000000000000openssl enc -d -aes256 -in fl@g.txt -out 1.txt-S: salt
模式攻击
ECB模式
最简单的加密模式即为电子密码本(Electronic codebook,ECB)模式。需要加密的消息按照块密码的块大小被分为数个块,并对每个块进行独立加密。
中间人攻击(MITM)
假如存在一个攻击者,当他作为中间人截获两方的通信时,他能够改变密文的分组顺序,当接收者对密文进行解密时,由于密文分组的顺序被改变了,因此相应的明文分组的顺序也被改变了,那么接收者实际上是解密出了一段被篡改后的密文。在这种场景中,攻击者不需要破译密码,也不需要知道分组密码的算法,他只需要知道哪个分组记录了什么样的数据。
参考:Boston Key Party CTF 2013 - MITM
1 | #python2 |
模式攻击
动态填充加密+枚举secret字符
方法一
1.明文由输入值m+flag+padding组成,$m$ 为空时, $c$ 可分 $k$ 块,不断调整 $m$ 的长度,直到 $m$ 长度为 $l+1$ 时 $c$ 可分 $k+1$ 块,那么说明 $m$ 长度为 $l$ 时 $c$ 刚好可分 $k$ 块,即无padding情况下,$m+flag$ 可分 $k$ 块,则flag长度即为 $8k-l$。
2.利用上面的思想,在 $m$ 长度为 $l$ 的基础上,长度不断加1,则可以把flag从后开始的每一位推到下一个块中,得到下一个块的密文 $c_i$;
3.又已爆破出的flag位+padding已知,则下一个块的构成为未知字符1位+已爆破出的flag位(+padding);
4.根据DES-ECB的性质,相同明文块对应的密文块相同。爆破第一位未知字符,将上面的块构成作为输入值输入,得到对应的密文的第一块,分别与实际密文 $c_i$ 比较,匹配的即为正确的明文字符。
5.以此类推,得到完整flag。
参考:
1 | from pwn import * |
方法二
1.由于是ECB的模式,所以当我们输入十五个’0’后,服务会将十五个’0’+flag加密,而此时第一组就是十五个’0’和flag的第一个字符。即,返回的明文的第一组是’0’*15 + flag[0]的密文。
2.我们遍历0-255,发送’0’*15+chr(i),看返回的密文是不是和最初获得的密文的第一组一致,如果一致,那么此时的chr(i)就是flag的第一位。
3.有了第一位我们就可以发送’0’*14+flag[0]过去,此时返回的第一组密文就是’0’*14+flag[0]+flag[1]的密文了,我们继续用第2步的方法就可以恢复flag[1]了。
4.如此循环往复,逐位爆破flag。
1 | def exp(): |
重排攻击
在块加密中ECB模式中每个块都是独立加密的。因此攻击者可以在未知密钥的情况下,对密文中的块进行重新排列,组合成合法的可解密的新密文。
考虑这么一种场景,某CMS的cookie格式为DES-ECB加密后的数据,而明文格式如下:
1 | admin=0;username=pan |
由于DES使用的块大小是8字节,因此上述明文可以切分成三个块,其中@为填充符号:
1 | admin=0; |
假设我们可以控制自己的用户名(在注册时),那么有什么办法可以在不知道密钥的情况下将自己提取为管理员呢(即admin=1)?首先将用户名设置为pan@@@@admin=1;,此时明文块的内容如下:
1 | admin=0; |
我们所需要做的,就是在加密完成后,将服务器返回的cookie使用最后一个块替换第一个块,这样一来就获得了一个具有管理员权限的合法cookie了。
CBC模式
IBM发明了密码分组链接(CBC,Cipher-block chaining)模式。在CBC模式中,每个明文块先与前一个密文块进行异或后,再进行加密。在这种方法中,每个密文块都依赖于它前面的所有明文块。同时,为了保证每条消息的唯一性,在第一个块中需要使用初始化向量。
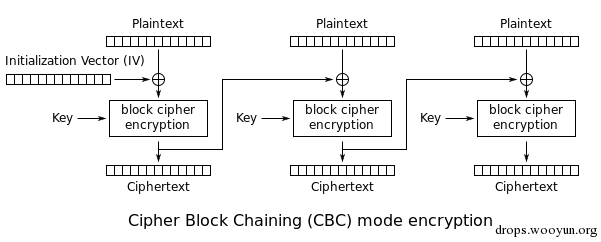
加密:
Ciphertext-0 = Encrypt(Plaintext XOR IV) ——只用于第一个组块
Ciphertext-N= Encrypt(Plaintext XOR Ciphertext-N-1) ——用于第二及剩下的组块
$\left\{\begin{array} {c} c_1 = \text{Enc}(m_1 \oplus \text{iv}) \newline c_2 = \text{Enc}(m_2 \oplus c_1) \newline \vdots \newline c_i = \text{Enc}(m_i \oplus c_{i-1}) \end{array} \right.$
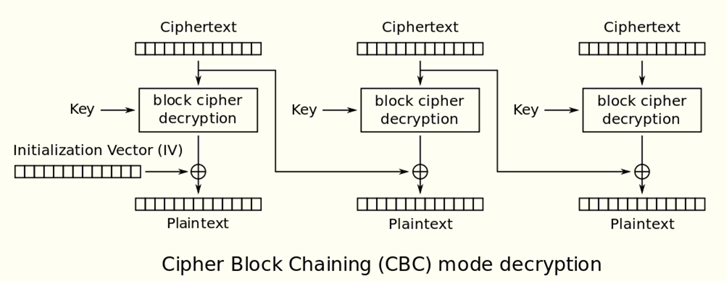
解密:
Plaintext-0 = Decrypt(Ciphertext) XOR IV ——只用于第一个组块
Plaintext-N= Decrypt(Ciphertext) XOR Ciphertext-N-1 ——用于第二及剩下的组块
$\left\{\begin{array} {c} m_1 = \text{Dec}(c_1)\oplus \text{iv} \newline m_2 = \text{Dec}(c_2)\oplus c_1 \newline \vdots \newline m_i = \text{Dec}(c_i)\oplus c_{i-1} \end{array} \right.$
CBC字节翻转
Plaintext:明文数据
IV:初始向量
Key:分组加密使用的密钥
Ciphertext:密文数据
每组解密时,先进行分组加密算法的解密,然后与前一组的密文进行异或才是最初的明文。
对于第一组则是与IV进行异或。
上一块密文用来产生下一块明文,如果改变上一块密文的一个字节,然后与下一个解密后的组块异或,就可以得到一个不同的明文。
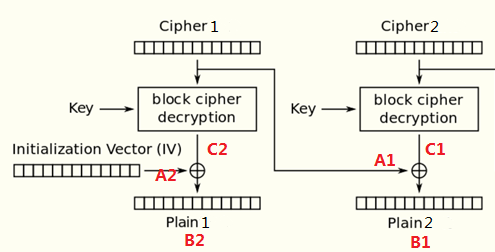
目标:要把Plain2中的某一字节翻转为另一字节。
由于C1来自于Cipher2进行Block Cipher Decryption之后的结果,而且Key未知,就不能直接得知C1的值;
但可通过字节翻转修改上一组密文Cipher1来翻转下一组的明文Plain2,从而可以完全忽视未知的C1值。
由异或运算可以推导:B1 = A1 ^ C1,则也有:C1 = A1 ^ B1
假设修改后的上一组密文为A1',要翻转的下一组明文为B1',则有:B1' = A1' ^ C1
如果能够修改Cipher1,那么就能够修改A1的值为A1',即A1' = A1 ^ B1 ^ B1'。
即:
1 | B = A ^ C |
要求:1. 对于A1完全可控;2. 已知B1的值。
由于修改了A1,Cipher1在进行Block Cipher Decryption的时候会得出错误的结果,再与IV异或会导致Plain1出错;
如果能够得到修改A1之后产生的错误的Plain1的值,而且IV可以完全控制的话,那么就能够再套用一次前面的方法。
即:
1 | B = A ^ C |
参考:SYPUCTF2020 - Yusa的密码学课堂—CBC第一课
1 | from pwn import * |
CBC字节翻转(Web)
1 | //原密文修改字符 |
Padding Oracle Attack
Padding Oracle Attack漏洞主要是由于设计使用的场景不当,导致可以利用密码算法通过”旁路攻击“被破解,利用该漏洞可以破解出密文的明文以及将明文加密成密文,该漏洞存在条件如下:
- 攻击者能够获取到密文(基于分组密码模式),以及IV向量(通常附带在密文前面,初始化向量)
- 攻击者能够修改密文触发解密过程,解密成功和解密失败存在差异性
根源
这个攻击的根源是明文分组和填充,同时应用程序对于填充异常的响应可以作为反馈,例如请求 http://www.example.com/decrypt.jsp?data=0000000000000000EFC2807233F9D7C097116BB33E813C5E,当攻击者在篡改data值时会有以下不同的响应:
- 如果data值没有被篡改,则解密成功,并且业务校验成功,响应200
- 如果data值被篡改,服务端无法完成解密,解密校验失败,则响应500
- 如果data值被篡改,但是服务端解密成功,但业务逻辑校验失败,则可能返回200或302等响应码,而不是响应500
攻击者只需要关注解密成功和解密失败的响应即可(第三种属于解密成功的响应),即可完成攻击。
破解明文
解密最后一个数据块,其结尾应该包含正确的填充序列。如果这点没有满足,那么加/解密程序就会抛出一个填充异常。Padding Oracle Attack的关键就是利用程序是否抛出异常来判断padding是否正确。
在不知道明文的情况下,如何猜解出明文?首先将密文分组,前面8个字节为初始化向量,后面16个字节为加密后的数据:
1 | 初始化向量:7B 21 6A 63 49 51 17 0F |
看如何通过构造前面初始向量来破解第一组密文:http://www.example.com/decrypt.jsp?data=7B216A634951170FF851D6CC68FC9537
- 将初始化向量全部设置为0,提交如下请求
http://www.example.com/decrypt.jsp?data=00000000000000000F851D6CC68FC9537,服务器势必会解密失败,返回HTTP 500,是因为在对数据进行解密的时候,明文最后一个字节的填充是0x3D,不满足填充规则,校验失败,此时示意图:
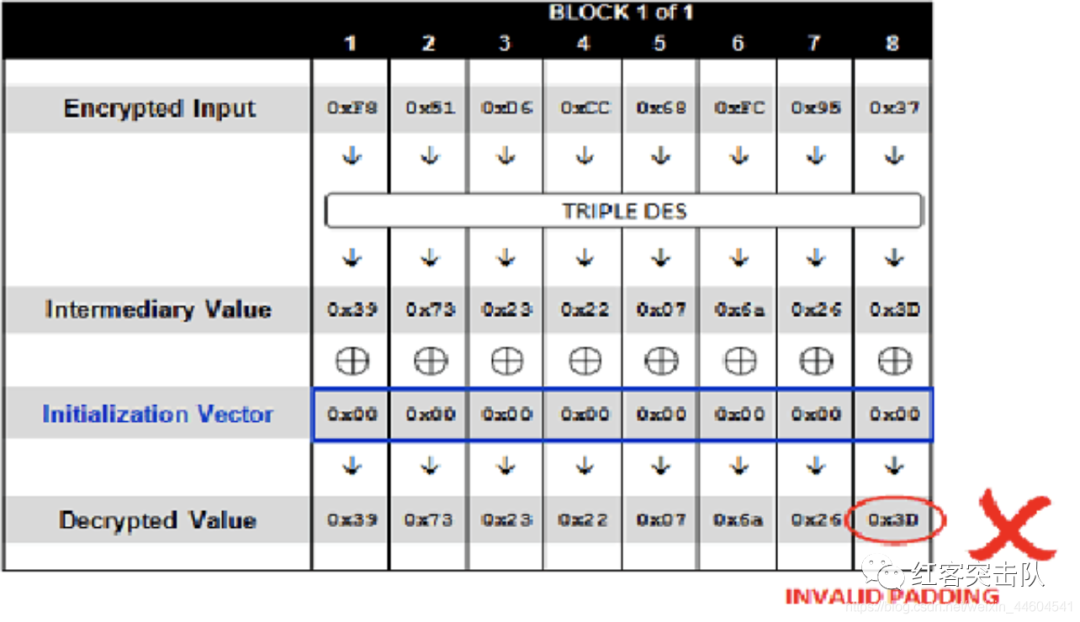
- 依次将初始化向量最后一个字节从
0x01~0xFF递增,直到解密的明文最后一个字节为0x01,成为一个正确的padding,当初始化向量为000000000000003C时,成功,服务器返回HTTP 200,解密示意图:
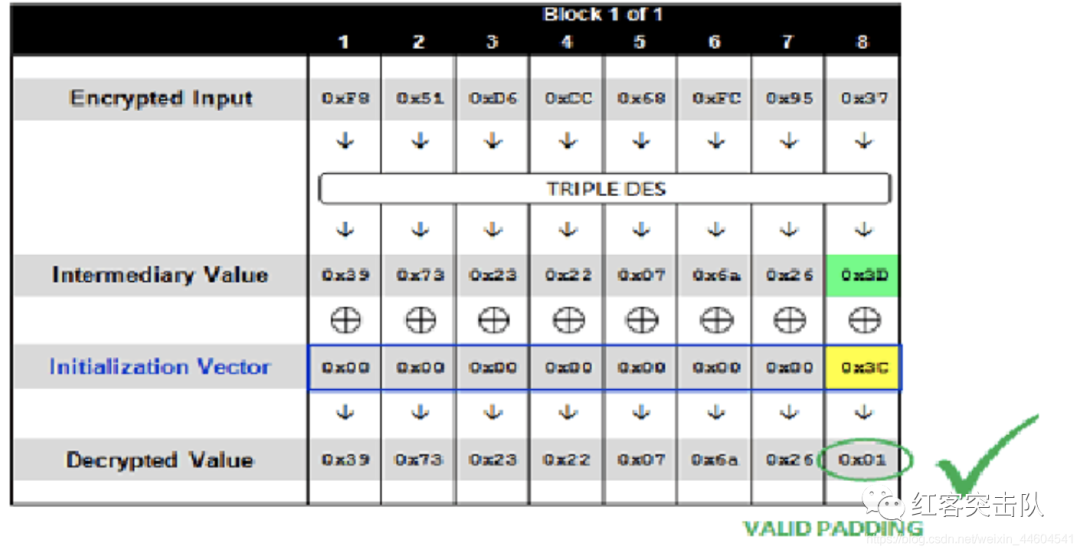
- 已知构造成功的IV最后一个字节为
0x3C,最后一个填充字符为0x01,则能通过XOR计算出,第一组密文解密后的中间值最后一个字节:0x01 xor 0x3C = 0x3D;重点:第一组密文解密的中间值是一直不变的,同样也是正确的,通过构造IV值,使得最后一位填充值满足0x01,符合padding规则,则意味着程序解密成功(当前解密的结果肯定不是原来的明文),通过循环测试的方法,猜解出中间值的最后一位,再利用同样的方式猜解前面的中间值,直到获取到完整的中间值。 - 下面将构造填充值为
0x02 0x02的场景,即存在2个填充字节,填充值为0x02,此时已经知道了中间值得最后一位为0x3D,计算出初始向量的最后一位为0x3D xor 0x02 = 0x3F,即初始向量为0000000000000003F,遍历倒数第二个字节从0x00~0xFF,直到响应成功,猜解出中间值得后两个字节分别为0x26 0x3D,示意图:

- 通过同样的方式,完成第一组密文中间值的猜解。
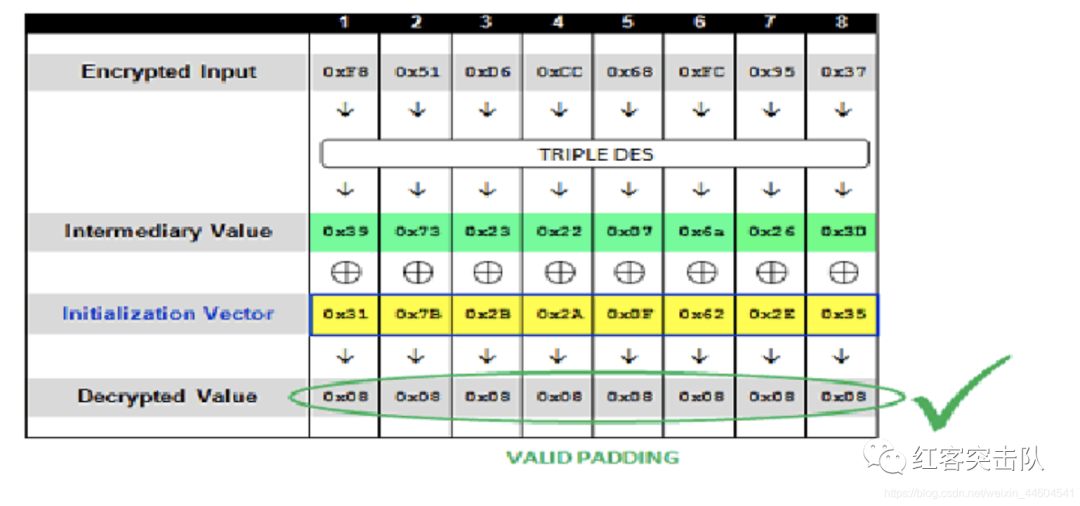
- 当第一组密文的中间值猜解成功后,将中间值和已知的IV做异或,则得到第一组密文的明文:
1 | 0x39 0x73 0x23 0x22 0x07 0x6A 0x26 0x3D |
- 续破解第二组密文,第二组密文的IV向量是第一组密文,按照上述的逻辑构造第一组密文,即可破解出第二组明文。
伪造密文
已经知道了中间值,那么只需传递指定的IV,就能制造任意想要的密文,如加密TEST:
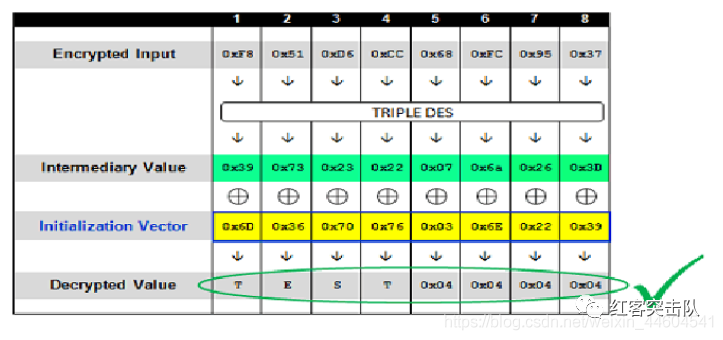
BP插件:PaddingOracleHunter
SM4
SM4是一种分组密码算法,其分组长度为128位(即16字节,4字),密钥长度也为128位(即16字节,4字)。其加解密过程采用了32轮迭代机制(与DES、AES类似),每一轮需要一个轮密钥(与DES、AES类似)。
1 | # Python |
1 | // C 脚本1 |
1 | // C 脚本2 |
Blowfish
Blowfish是一个对称加密块算法,由Bruce Schneider于1993年设计,现已应用在多种加密产品。Blowfish能保证很好的加密速度,并且目前为止没有发现有效地破解方法。目前为止AES比Blowfish有更广的知名度。
BlowFish参考:https://github.com/Rupan/blowfish/blob/master/blowfish.c

