ECC
椭圆曲线密码学（英语：Elliptic Curve Cryptography，缩写：ECC）是一种基于椭圆曲线数学的公开密钥加密算法。与传统的基于大质数因子分解困难性的加密方法不同，ECC 依赖于解决椭圆曲线离散对数问题的困难性。它的优势主要在于相对于其它方法，它可以在使用较短密钥长度的同时保持相同的密码强度。目前椭圆曲线主要采用的有限域有以素数为模的整数域 $\text{GF}(p)$和特征为2的伽罗华域 $\text{GF}(2^m)$。
椭圆曲线
椭圆曲线的定义式：$y^2+axy+by=x^3+cx^2+dx+e$
一般方程：$y^2+a_1xy+a_3y=x^3+a_2x^2+a_4x+a_6$
最常用方程（维尔斯特拉斯标准形式）
$y^2=x^3+ax+b$，判别式 $\Delta=-16(4a^3+27b^2)\neq 0$
椭圆曲线的定义也要求曲线是非奇异的。几何上来说，这意味着图像里面没有尖点、自相交或孤立点。代数上来说，这成立当且仅当判别式 $\Delta \neq 0$。
还需要一个无穷远点作为曲线的一部分，用 $\text{O}$ 表示。
椭圆曲线表达式
$\{(x,y) \in \mathbb{R}^2 \mid y^2=x^3+ax+b,4a^3+27b^2\neq0\} \cup \{\text{O}\}$
椭圆曲线阿尔贝群
$\text{O}$ 为零元，相反数 $P$ 为关于X轴对称的另一边的点，加法规则为直线三点 $P+Q+R=0$。
几何加法
普通相交三点：$P+Q+R=0$
普通相交两点：$P+P+Q=0$，$P+Q+Q=0$ （一点相切）
垂直相交两点：$P+Q+0=0$ （垂直X轴）
垂直相交一点：$P+P+0=0$ （垂直X轴+一点相切）
代数加法
去掉特殊情况，只考虑两个非零非对称的点 $P=(x_P,y_P)$ 和 $Q=(x_Q,y_Q)$。
若 $P$ 和 $Q$ 不同，即 $x_P \neq x_Q$，直线斜率 $k=\cfrac{y_P-y_Q}{x_P-x_Q}$
若 $P$ 和 $Q$ 相同，即 $x_P =x_Q$，直线斜率 $k=\cfrac{3x_P^2+a}{2y_P}$
这条直线和椭圆曲线的交点 $R=(x_R,y_R)$，则：
$x_R=k^2-x_P-x_Q$
$y_R=y_P+k(x_R-x_P)=y_Q+k(x_R-x_Q)$
于是：$P+Q=(x_P,y_P)+(x_Q,y_Q)=-R=(x_R,-y_R)$
标量积（点积/数乘/倍乘）
$Q=nP=P+P+\cdots+P=\sum_{i=0}^{n-1}(b_i\cdot2^i)P,\quad b_i=\{0,1\}$，$b_i$ 为 $n$ 的各比特位值。
对数
$Q=nP$，已知 $Q,P$，求 $n$。
有限域椭圆曲线
椭圆曲线是连续的，并不适合用于加密，所以必须把椭圆曲线变成离散的点，把椭圆曲线定义在有限域上。
有限域上的椭圆曲线是指在椭圆曲线的定义式中，所有的系数都是在某个有限域 $\text{GF}(p)$ 中的元素，其中 $p$ 为一个大素数。
给出一个有限域 $\text{F}p$，
- $\text{F}p$ 中有 $p$（$p$ 为质数）个元素 $0,1,2,\cdots,p-1$；
- $\text{F}p$ 的加法是 $a+b \equiv c \pmod p$；
- $\text{F}p$ 的乘法是 $a\times b \equiv c \pmod p$；
- $\text{F}p$ 的除法是 $\cfrac{a}{b} \equiv c \pmod p$，即 $a \times b^{-1} \equiv c \pmod p$，$b^{-1}$ 为 $b$ 的逆元，满足 $b \times b^{-1} \equiv 1 \pmod p$；
- $\text{F}p$ 的单位元是 $1$，零元是 $\text{O}$；
- $\text{F}p$ 域内运算满足交换律、结合律、分配率。
椭圆曲线 $\text{E}p(a,b)$，$p$ 为质数，$x,y \in [0,p-1]$：$y^2=x^3+ax+b \pmod p$，
选择两个满足下列约束条件的小于 $p$ 的非负整数 $a,b$：$4a^3+27b^2 \neq 0 \pmod p$。
$\text{F}p$ 上的椭圆曲线同样有加法：
无穷远点 $\text{O}$ 是零元，有 $\text{O}+\text{O}=\text{O}$，$\text{O}+P=P$；
$P(x,y)$ 的负元是 $(x,-y \bmod p)=(x,p-y)$，有 $P+(-P)=\text{O}$；
$P(x_1,y_1),Q(x_2,y_2)$ 的和 $R(x_3,y_3)$ 有如下关系：
$x_3 \equiv k^2-x_1-x_2 \pmod p$
$y_3 \equiv k(x_1-x_3)-y_1 \pmod p$
若 $P=Q$ 则 $k=\cfrac{3x_1^2+a}{2y_1}\pmod p$；
若 $P \neq Q$ 则 $k=\cfrac{y_2-y_1}{x_2-x_1} \pmod p$。
点的阶
如果椭圆曲线上一点 $P$，存在最小的正整数 $n$ 使得数乘 $nP=\text{O}$ ，则将 $n$ 称为 $P$ 的阶；若 $n$ 不存在，则 $P$ 是无限阶的。
加密原理
考虑 $K=kG$ ，其中 $K,G$ 为椭圆曲线 $\text{E}p(a,b)$ 上的点，$n$ 为 $G$ 的阶（$nG=\text{O}$），$k$ 为小于 $n$ 的整数。
给定 $k$ 和 $G$ ，根据加法法则，计算 $K$ 很容易，但反过来，给定 $K$ 和 $G$，求 $k$ 就非常困难。因为实际使用中的ECC原则上把 $p$ 取得相当大，$n$ 也相当大，要把 $n$ 个解点逐一算出来列成上表是不可能的。
这就是椭圆曲线加密算法的数学依据。
点 $G$ 称为基点 (base point)，$k$ ($k<n$) 为私有密钥 (private key)，$K$ 为公开密钥 (public key)。
通信算法
A选定一条椭圆曲线 $\text{E}p(a,b)$，并取椭圆曲线上一点作为基点 $G$；
A选择一个私有密钥 $k$ ($k<n$)，并生成公开密钥 $K=kG$；
A将 $\text{E}p(a,b)$ 和点 $K,G$ 传给B；
B收到信息后，将待传输的明文编码到 $\text{E}p(a,b)$ 上的一点 $M$，并产生一个随机整数 $r$（$r<n$，$n$ 为 $G$ 的阶数）；
B计算点 $C_1=M+rK$ 和 $C_2=rG$；
B将 $C_1,C_2$ 传给A；
A收到信息后，计算 $C_1-kC_2$，结果就应该是点 $M$。
（$C_1-kC_2=M+rK-krG=M+rkG-krG=M$）
1 | #Sage |
参考
ECC椭圆曲线密码学的原理、公式推导、例子、Python实现和应用
常见攻击
Smart’s attack
适用情况：$\text{E.order}()=p$。
1 | p = |
Invalid curve attack
服务端并没有检查输入的点是否在原曲线 $E:y^2 = x^3 + ax + b \pmod p$ 上，存在 Invalid Curve Attack。
由于 Elliptic Curve 的点加运算、标量乘法都与 $E$ 的参数 $b$ 无关，只与 $a$ 有关，所以可以通过平移曲线 $E$ 到 $E’:y^2 = x^3 + ax + b’ \pmod p$ 上，这样不会改变群的运算，但是 $E’$ 的阶会发生改变，只要 $E’$ 的阶足够光滑，或者有小的素因子，就可以求解（子群上）DLP，最后再用 CRT 恢复出服务端私钥。一般来说阶的最大素因子小于 $2^{50}$ ，就能很快（几分钟）跑出 DLP。
1 | def get_invalid_point(p, a, known_factors = [], check_point = False): |
参考：
NCTF 2023 - Code Infinite
ECDLP
ECDLP即椭圆曲线上的离散对数问题（The Elliptic Curve Discrete Logarithm Problem）。
椭圆曲线上离散对数问题ECDLP定义如下：给定素数 $p$ 和椭圆曲线 $E$，对 $Q=kP$，在已知 $P,Q$ 的情况下求出小于 $p$ 的正整数 $k$。可以证明由 $k$ 和 $P$ 计算 $Q$ 比较容易，而由 $Q$ 和 $P$ 计算 $k$ 则比较困难。
将椭圆曲线中的加法运算与离散对数中的模乘运算相对应，将椭圆曲线中的乘法运算与离散对数中的模幂运算相对应，我们就可以建立基于椭圆曲线的对应的密码体制。
1 | #Sage Code 1 |
Pohlig-Hellman算法
算法由Pohlig和Hellman发明，这是一种为解决离散对数问题而提出的攻击方法，早在1978年就被提出。主要思想是对阶数进行分解，比如整数域中 $y = g^x \pmod p$ 里的 $x$ 以及椭圆曲线离散对数问题中 $Gk = Q$ 的 $G$ 的阶 $n$，这样就把对应的离散对数问题转移到了每个因子条件下对应的离散对数，然后可以利用中国剩余定理进行求解。
假设需要求解的式子为 $Q=lP$，其中 $P$ 为选取的一个基点， $l$ 为选定的随机数，相当于要求解的私钥。
首先求得 $P$ 的阶 $n$ ，即可使得 $nP$ 不存在的最小正整数，将 $n$ 进行分解，设 $n=p_1^{e_1}p_2^{e_2}\cdots p_r^{e_r}$，
将因子取出，计算 $l_i \equiv l \pmod {p_i^{e_i}},\quad i \in [1,r]$，即
$\begin{cases} l \equiv l_1 \pmod {p_1^{e_1}} \newline l \equiv l_2 \pmod {p_2^{e_2}} \newline {\vdots} \newline l \equiv l_r \pmod {p_r^{e_r}} \end{cases}$
如果得到 $l_i(i \in [1,r])$ 的值就能使用中国剩余定理进行求解得到 $l$，下面求解 $l_i$。
首先将 $l_i$ 设为 $p_i$ 表示的多项式 $l_i=z_0+z_1p_i+z_2p_i^2+ \cdots +z_{e-1}p_i^{e-1}, \quad z \in [0,p_i-1]$，
为计算 $z_i$，分别取 $P_0$ 和 $Q_0$，并取值 $P_0=\cfrac{n}{p_i}P,\quad Q_0=\cfrac{n}{p_i}Q$，
这样有 $p_iP_0=nP$，则可得到 $Q_0=\cfrac{n}{p_i}Q=\cfrac{n}{p_i}(lP)=l(\cfrac{n}{p_i}P)=lP_0$，相当于在原表达式的两边乘上 $\cfrac{n}{p_i}$，
再转回 $l_i$，先求解 $z_0$：
$l_iP=Q \\\Rightarrow l_iP_0=Q_0 \\\Rightarrow (z_0+z_1p_i+\cdots+z_{e-1}p_i^{e-1})P_0=Q_0 \\\Rightarrow z_0P_0=Q_0$
这时便将在 $P$ 域上的离散对数分解到了 $P_0$ 域上，因为 $P_0$ 的阶是 $p_i$，已经较原本的阶 $n$ 运算的复杂度小了很多，当然，除非 $n$ 本身就是个大素数。
求得 $z_0$，再代回原式：
$(z_0+z_1p_i+\cdots+z_{e-1}p_i^{e-1})P_0=Q_0 \\\Rightarrow z_0P_0+(z_1p_i+\cdots+z_{e-1}p_i^{e-1})P_0=Q_0 \\\Rightarrow (z_1p_i+\cdots+z_{e-1}p_i^{e-1})P_0=Q_0-z_0P_0 \\\Rightarrow z_1p_i=Q_0-z_0P_0$
此时就可以求解 $z_1$，然后依次将 $z_i$ 全部算出来，这样我们就得到了 $l_1$，然后便可以代入前面的等式，将 $l_i$ 都求出后即可利用中国剩余定理求出 $l$。
1 | #Sage Code 1 |
1 | #Sage Code 2 |
ECDH
椭圆曲线迪菲-赫尔曼密钥交换（英语：Elliptic Curve Diffie–Hellman key exchange，缩写为ECDH），是一种匿名的密钥合意协议（Key-agreement protocol），这是迪菲-赫尔曼密钥交换的变种，采用椭圆曲线密码学来加强性能与安全性。在这个协定下，双方利用由椭圆曲线密码学建立的公钥与私钥对，在一个不安全的通道中，建立起安全的共有加密资料。
ECDH一般来说交换的都是私钥，这个密钥一般作为“对称加密”的密钥而被双方在后续数据传输中使用。
ECDH是建立在这样一个前提之上的，给定椭圆曲线上的一个点 $P$，一个整数 $k$，求 $Q=kP$ 很容易；但是通过$Q,P$ 求解 $k$ 很难。
算法描述
- A和B双方约定使用ECDH秘钥交换算法，这个时候双方也知道了ECDH算法里的一个大素数 $p$，这个 $p$ 可以看做是一个算法中的常量，$p$ 的位数决定了攻击者破解的难度。还有一个整数 $g$ 用来辅助整个秘钥交换，$g$ 不用很大，双方知道 $g$ 和 $p$ 之后就开始了ECDH交换秘钥的过程。
- A知道了共用参数 $p$ 和 $g$，生成整数 $a$ 作为私钥，A利用 $p,g,a$ 通过公式 $g^a \bmod p = A$ 生成 $A$ 作为公钥传递。
- B通过链路收到A发来的 $p,g,A$，知道了A的公钥 $A$。这个时候B也生成自己的私钥 $b$，然后通过公式 $g^b \bmod p = B$ 生成自己公钥 $B$。 在发送公钥 $B$ 前，B通过 $A^b \bmod p = K$ 生成 $K$ 作为公共密钥，但是并不发送给A。
- A收到B发来的公钥 $B$ 以后，同样通过 $B^a \bmod p = K$ 生成公共密钥 $K$，这样A和B就通过不传递私钥 $a$ 和 $b$ 完成了对公共密钥 $K$ 的协商。
中间人只知道 $A$ 和 $B$ 以及椭圆曲线的公共参数，是无法算出共享密钥 $K$ 的。
这其实就是迪菲-赫尔曼问题：给定三个点 $P,aP,bP$，那么 $abP$ 的结果是什么？
或者可以这么理解：给定三个整数 $k,k^x,k^y$，那么 $k^{xy}$ 的结果是什么？
参考
攻击
中间人攻击（MITM）
ECElGamal
在密码学中，ElGamal加密算法是一个基于迪菲-赫尔曼密钥交换的非对称加密算法。GnuPG和PGP等很多密码学系统中都应用到了ElGamal算法。
ElGamal加密算法可以定义在任何循环群 $G$ 上。它的安全性取决于 $G$ 上的离散对数难题。
密钥生成
选取一条椭圆曲线 $\text{E}_p(a,b)$，将明文消息 $m$ 嵌入到曲线上的点 $P_m$，再对点 $P_m$ 做加密变换。
取 $\text{E}_p(a,b)$ 的一个生成元（基点） $G$， $\text{E}_p(a,b)$ 和 $G$ 作为公开参数。
A选 $n_A$ 作为密钥，以 $P_A=n_AG$ 作为公钥。
加密过程
用户B向A发送消息 $P_m$，选取一个随机的正整数 $k$，产生以下点对作为密文：
$C_m=(kG,P_m+kP_A)$。
解密过程
A以密文点对中的第二个点，减去用自己的密钥与第一个点的倍乘，即：
$P_m+kP_A-n_AkG=P_m+k(n_AG)-n_AkG=P_m$。
ECDSA
椭圆曲线数字签名算法（英语：Elliptic Curve Digital Signature Algorithm，缩写：ECDSA）是一种基于椭圆曲线密码学的公开密钥加密算法。
ECDSA是DSA作用于椭圆曲线的一个变种算法。A和B仍然使用同样的曲线，ECDSA需要使用明文的哈希结果，而不是明文本身。哈希函数的选择取决于使用者，但是需要明确的是必须选择加密安全的哈希函数。
场景：Alice 想要使用她的私钥 $d_A$ 来签名，Bob 想用 Alice 的公钥 $H_A$ 要验证签名（$H_A=d_AG$），只有 Alice 才能提供正确的签名，而每个人都可以验证签名。
签名过程
A使用算法来签名的步骤：
- 选取一条椭圆曲线 $\text{E}_p(a,b)$；
- 选取一个随机数 $k\quad (k\in[1,n-1])$ (Nonce)，$n$ 为 $\text{E}_p(a,b)$ 的阶；
- 选取 $\text{E}_p(a,b)$ 的一个基点 $G$，计算点 $K=kG$，坐标表示为 $K=(x_K,y_K)$；
- 计算数字 $r=x_K \bmod n$；
- 如果 $r=0$，另选一个 $k$ 并重新计算；
- 获取数据 $M$ 的Hash值，记为$z=\text{Hash}(M)$，计算 $s=k^{-1}(z+rd_A) \bmod n$；
- 如果 $s=0$，另选一个 $k$ 并重新计算；
- 输出签名 $(r,s)$。
通俗的说，这个算法一开始生成了 $k$，得益于点乘，$k$ 被隐藏在了 $r$ 中，然后通过 $s$ 的等式将 $r$ 绑定到了消息散列值 $z$ 上。
为了计算 $s$，必须计算 $k^{-1} \bmod n$，只有在 $n$ 是素数的情况下才能保证这一过程，如果子群的阶不是一个素数，ECDSA 将不起作用。
验证过程
为了验证签名，需要A的公钥 $H_A$、哈希值 $z$ 和签名 $(r,s)$。
- 计算整数 $u_1=s^{-1}z \bmod n$；
- 计算整数 $u_2=s^{-1}r \bmod n$；
- 计算点 $P=u_1G+u_2H_A=(s^{-1}zG+s^{-1}rH_A) \bmod n=s^{-1}G(z+rd_A) \bmod n$；
- 只有当 $r=x_P \bmod n$ 的时候，签名才被成功验证。
参考
攻击
$k$ 复用（共享 $k$）
参考DSA攻击。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92from gmpy2 import invert
from hashlib import sha256, sha1
from pwn import *
from parse import *
from pwnlib.util.iters import bruteforce
import string, random
import ecdsa
context(os="linux", arch="amd64", log_level="debug")
HOST = "127.0.0.1"
PORT = 10305
r = remote(HOST, PORT)
def brute_force(prefix,s):
return bruteforce(lambda x:sha256(x+prefix).hexdigest()==s,string.ascii_letters+string.digits,length=4,method='fixed')
def recv(keepends=False):
return r.recvline(keepends=keepends).strip()
def send(anti, msg):
r.sendlineafter(anti, msg)
def sendHash():
context = recv()
prefix, s = parse("sha256(XXXX+{}) == {}",context)
proof = brute_force(prefix,s)
send("Give me XXXX:", proof)
def getMessage():
recv()
recv()
msg1 = recv()[-64:]
msg2 = recv()[-64:]
return msg1, msg2
def calculator(msg1, msg2):
curve = ecdsa.curves.SECP256k1
G = curve.generator
n = G.order()
r = 0
while r == 0:
random_k = ecdsa.util.randrange(n)
k = random_k % n
ks = k + n
kt = ks + n
if ecdsa.util.bit_length(ks) == ecdsa.util.bit_length(n):
p1 = kt * G
else:
p1 = ks * G
r = p1.x() % n
h1 = ecdsa.util.string_to_number(sha1(msg1).digest()) % n
h2 = ecdsa.util.string_to_number(sha1(msg2).digest()) % n
x = ((-(h1 + h2)) * invert(2*r, n)) % n
prikey = ecdsa.SigningKey.from_secret_exponent(x, ecdsa.curves.SECP256k1, hashfunc=sha1)
pubkey = prikey.get_verifying_key()
send("Please choice your options:", "3")
send("Please give me your public_key(hex):", pubkey.to_string().encode('hex'))
sign = prikey.sign(msg1, k = k)
send("Please choice your options:", "5")
send("Please give me the message(hex):", msg1.encode('hex'))
send("Please give me the signature(hex):", sign.encode('hex'))
if "Verify successfully!" in recv():
print ("msg1 verify successfully!")
send("Please choice your options:", "5")
send("Please give me the message(hex):", msg2.encode('hex'))
send("Please give me the signature(hex):", sign.encode('hex'))
if "Verify successfully!" in recv():
print ("msg2 verify successfully!")
send("Please choice your options:", "6")
send("Please give me the signature(hex) of the frist message:", sign.encode('hex'))
send("Please give me the signature(hex) of the second message:", sign.encode('hex'))
def main():
sendHash()
msg1, msg2 = getMessage()
calculator(msg1, msg2)
r.recvuntil("}")
r.close()
if __name__ == '__main__':
main()$k$ 部分泄露+多组 $(r,s)$ 签名
Recovering cryptographic keys from partial
Pbctf 2020 - LeaK
DownUnderCTF 2020 - impECCable
L3HCTF - EzECDSA
LLL算法。
$k$ 低位相同+多组 $(r,s)$ 签名
GFCTF2021 - Wtfcrypto
Dual EC DRBG
双椭圆曲线确定性随机数发生器（Dual_EC_DRBG），也被称作双椭圆曲线随机数发生器，是一种使用椭圆曲线密码学实现的密码学安全伪随机数发生器（CSPRNG）。它的设计者是 NSA，2006 年它被 NIST 作为标准，到 2014 年被移除。
攻击
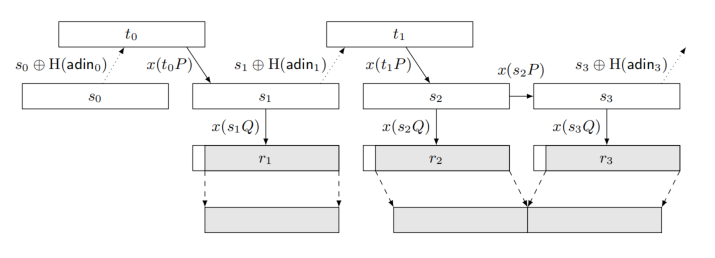
后门原理：
$P=dQ$ 关系中的 $d$ 如果被攻击者知道了，那么攻击者就可以利用 $d$ 构造出之后每一步的 $\text{state}$，从而可以成功预测每一步的 $r_i$，这个随机数生成器也就被攻破了。
设每一步的 $\text{state}$ 为 $s_i$，随机数为 $r_i$，随机数对应的椭圆曲线上的点为 $R_i$。
那么对于攻击者来说，已知 $P$、$Q$、$d$、$R_i$，而 $s_i$ 未知。于是有：
$\begin{cases} ((s_i \cdot P)_x \cdot P)_x & \rightarrow s_{i+1} \newline ((s_i \cdot P)_x \cdot Q)_x & \rightarrow r_i \end{cases}$
显然，我们需要求得某一步的 $s_i$，那么之后每一步的 $s_i$ 就都知道了，从而之后的 $r_i$ 我们也都可以预测了。
而论文里的后门就是构造 $d \cdot r_{i-1}$，其恰好是 $s_i$，于是看似安全的体制就被攻破了。
记 $k_i = (s_i \cdot P)_x$，有：
$\begin{align} d \cdot r_{i-1} & = {(d \cdot R_{i-1})_x = (d \cdot k_{i-1} \cdot Q)_x} = {(k_{i-1} \cdot d \cdot Q)_x = (k_{i-1} \cdot P)_x} = {((s_{i-1} \cdot P)_x \cdot P)_x = s_i} \end{align}$
1 | def do_next(s): |
参考
Dual EC: A Standardized Back Door
UTCTF 2021 - Sleeves
EC-LCG
给出ECC的7个点的 $x$ 坐标值，满足 $X_i=X_{i-1}+b$，得到关于 $x_b,a,b$ 三个未知数有关的方程，一共6个方程，用Gröbner基求解 $C=kp$。
参考
PREDICTING THE ELLIPTIC CURVE CONGRUENTIAL GENERATOR
RCTF 2022 - IS_THIS_LCG?
ECDDHP
椭圆曲线上的DDH问题（Elliptic Curve Decisional Diffie-Hellman Problem，ECDDHP）。
双线性对满足 $e(aG,bG)=e(G,abG)$。
如果随便选一个椭圆曲线点群，ECDDH假设通常是不成立的，并且攻击方法就很简单：看等式 $e(aG,bG)=e(G,abG)$ 是否成立。
1 | # sage |
标准椭圆曲线
NIST P-256
1 | NIST_256 = ( |
NIST P-512
1 | NIST_521 = ( |
