RoarCTF 2020

match 评论

​

由嘶吼主办的2020 RoarCTF线上赛，平台：https://ctf.4hou.com/。

Rank: 27

赛后无环境复现，故每题未写上flag值。

Misc

签到题

不属于Misc分类也不像签到题的签到题。

F12查看源码，发现/?url，需要GET方式传url。

尝试目录穿越及远程请求数据无效，发现file伪协议/?url=file:///etc/passwd能成功回显内容，

读index.php源码：/?url=file:///var/www/html/index.php，内容为PHP curl实现，过滤了flag关键字。

利用PHP的二次编码解析bug（bypass strpos verification）编码即可绕过过滤：

Payload:/?url=file:///fla%2567

​

Hi_433MHz

RF射频信号数据，以原始数据方式导入Audacity查看波形，放大，

发现摩斯密码，对照可能的flag字符串摩斯密码--..--./--.--../--....-/--..---，开头四段去掉前后的.是吻合的，手工记录所有段解密得flag。

​

FM

FM调频信号数据，以原始数据方式导入Audacity查看波形未查出有用信息。

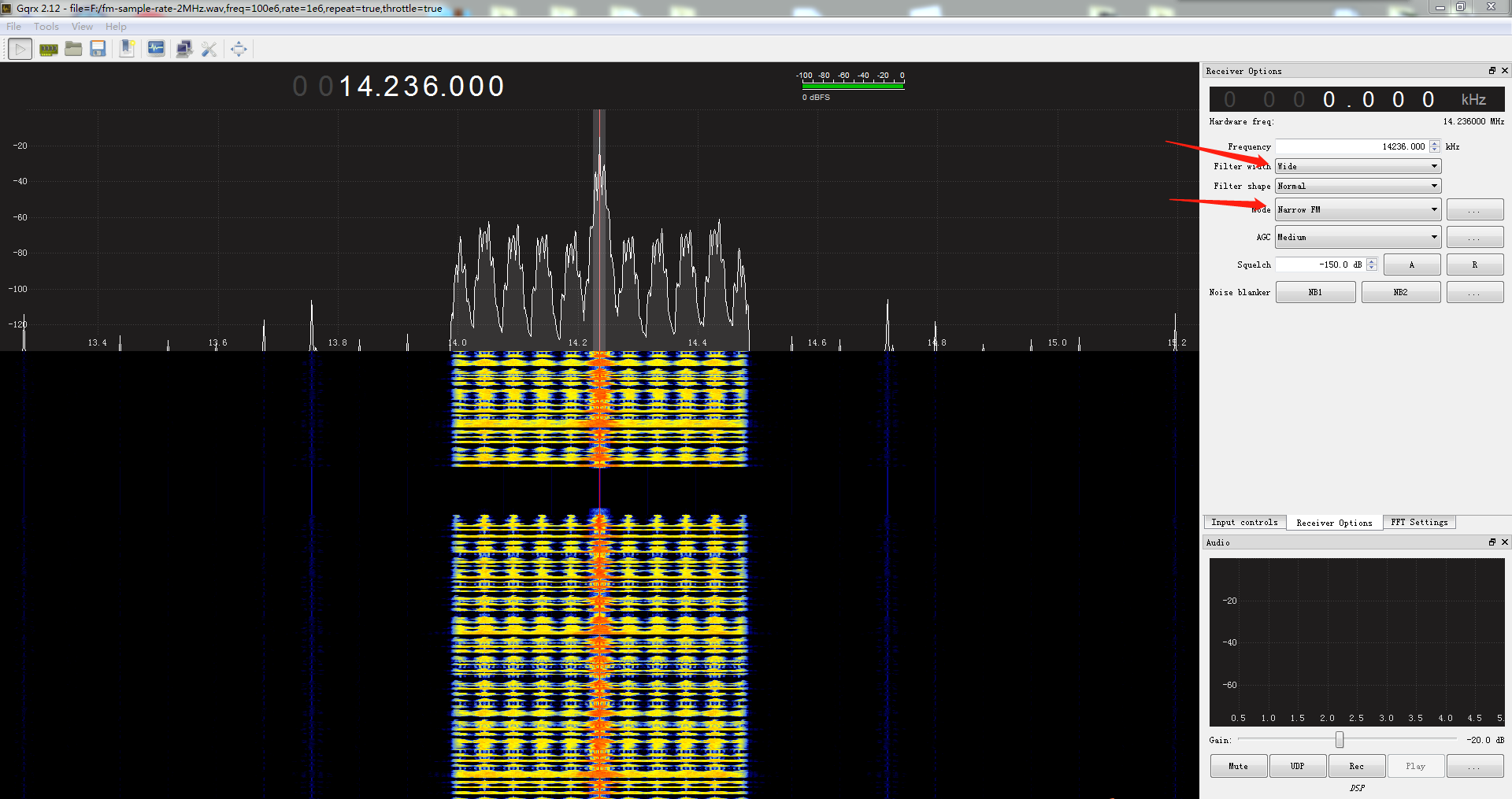
搜索可查看FM信号的软件，首先尝试用SDR#打开，设定好2MHz的采样率，调整频率至幅值最高处，能勉强听到人声，但噪声太大，官方原生版SDR#也未找到比较好的去噪滤波功能。

换一个软件，找到Windows平台SDR软件全家桶PothosSDR，使用里面的GQRX SDR分析，功能齐全，导入后调整 Mode=Narrow FM 及 Filter width=Wide，可以清晰听出内容，报的就是flag。

fm-GQRX SDR

​

Crypto

Crypto_System

从CyBRICS 2020 - Too Secure魔改的Pedersen加密，算法描述：

CyBRICS 2020-Too Secure

已知信息 $m_1,m_2$和 $m_1$ 的 $r_1$，$m_1$ 通过因子 $r_1$ 加密得到 $c_1$，需要求出因子 $r_2$，使得 $m_2$ 通过 $r_2$ 加密得到的 $c_2$ 与 $c_1$ 相同，即产生碰撞。

对于待加密信息 $m_1$，$c_1=g^{m_1}h_1^{r_1}$，注意到 $h_1=g^{a_1}$，故 $c_1=g^{m_1+a_1r_1}$；

要碰撞信息 $m_2$ 的因子 $r_2$ 应满足 $c_2=c_1$，即 $m_1+a_1r_1 \equiv m_2+a_2r_2 \pmod {\varphi(p)}$，

又 $q$ 为 $g$ 的阶，所以有 $m_1+a_1r_1 \equiv m_2+a_2r_2 \pmod q$，

故 $r_2 \equiv (m_1+a_1r_1-m_2) \pmod q$，即可求出 $r_2$。

Exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#python2
from pwn import *
from parse import *
from pwnlib.util.iters import bruteforce
import string
from hashlib import sha256
from Crypto.Util.number import *
import hashlib
from gmpy2 import gcd,invert

def brute_force(prefix,s):
	return bruteforce(lambda x:sha256(x+prefix).hexdigest()==s,string.ascii_letters+string.digits,length=4,method='fixed')

p = 12039102490128509125925019010000012423515617235219127649182470182570195018265927223
g = 10729072579307052184848302322451332192456229619044181105063011741516558110216720725

def int2str(data, mode="big"):
    if mode == "little":
        return sum([ord(data[_]) * 2 ** (8 * _) for _ in range(len(data))])
    elif mode == "big":
        return sum([ord(data[::-1][_]) * 2 ** (8 * _) for _ in range(len(data))])

def get_parameter(m):
    x = int2str(m, 'little')
    y = pow(g, x, p)
    a = bytes_to_long(hashlib.sha256(long_to_bytes(y).rjust(128, "\0")).digest())
    b = pow(a, a, p - 1)
    h = pow(g, b, p)
    return x, y, h, b

def sign(m, r):
    x, y, h, b = get_parameter(m)
    s = (y * pow(h, r, p)) % p 
    return s

def verify(m, r, s):
    x, y, h, b = get_parameter(m)
    if s == ((y * pow(h, r, p)) % p):
        return True
    else:
        return False

r=remote('139.129.98.9',30001)
data = r.recvline()
prefix, s = parse("sha256(XXXX+{}) == {}",data)
r.recvuntil('Give me XXXX:')
r.sendline(brute_force(prefix,s))

r.recvline()
r.recvline()
m1 = long_to_bytes(int(parse("Here is the frist message(64 bytes):{}",r.recvline())[0],16))
m2 = long_to_bytes(int(parse("Here is the second message(64 bytes):{}",r.recvline())[0],16))
r1 = int(parse("The frist message's 'r':{}",r.recvline())[0])
print(m1)
print(m2)

#sage solve order q:  g^q=1(mod p) 
q = 1039300813886545966418005631983853921163721828798787466771912919828750891
assert(pow(g, q, p) == 1)
assert(gcd(q, p-1) == q)

M1,y1,h1,b1 = get_parameter(m1)
M2,y2,h2,b2 = get_parameter(m2)

s1 = sign(m1, r1)

p1 = b1*r1
p2 = M2-M1
p3 = p1-p2
p4 = invert(b2,q)
r2 = (p3*p4)%q
s2 = sign(m2,r2)

if s1==s2:
	print('r1 = '+str(r1))
	print('r2 = '+str(r2))
	print('s1 = '+str(s1))
	print('s2 = '+str(s2))
	print('verify(m2,r2,s2) = '+str(verify(m2,r2,s2)))

r.recvuntil('Please choice your options:')
r.sendline('3')
r.sendlineafter('Please give me the (r,s) of the second message:','('+str(r2)+','+str(s2)+')')
print(r.recvall())

​

Reverse

task.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
from gmpy2 import *
from secret import *

assert(flag.decode().startswith('flag{')) and (flag.decode().endswith('}'))
def reverse(x):
	y = 0
	while x != 0:
		y = y*2 + x%2
		x = x // 2
	return y


while True:
	p = getStrongPrime(512)
	q = reverse(p)
	if is_prime(q):
		break

n = p*q
e = 65537
m = bytes_to_long(flag)
enc = powmod(m,e,n)
#n = 158985980192501034004997692253209315116841431063210516613522548452327355222295231366801286879768949611058043390843949610463241574886852164907094966008463721486557469253652940169060186477803255769516068561042756903927308078335838348784208212701919950712557406983012026654876481867000537670622886437968839524889
#enc = 103728452309804750381455306214814700768557462686461157761076359181984554990431665209165298725569861567865645228742739676539208228770740802323555281253638825837621845841771677911598039696705908004858472132222470347720085501572979109563593281375095145984000628623881592799662103680478967594601571867412886606745

ASIS 2015 - RSASR魔改， $q$ 是 $p$ 的2进制反素数（emirp数），bin(q)=bin(p)[::-1]。

利用回溯算法按位从最高位端向中间爆破。

Exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#python2
n = 158985980192501034004997692253209315116841431063210516613522548452327355222295231366801286879768949611058043390843949610463241574886852164907094966008463721486557469253652940169060186477803255769516068561042756903927308078335838348784208212701919950712557406983012026654876481867000537670622886437968839524889
def t(a, b, k):
	# sqrt(n)有512位2进制位, 需计算高低位每边的256位
    if k == 256:
        if a*b == n:
            print(a, b)
        return
    for i in xrange(2):
        for j in xrange(2):
			# 对两个素数因子尝试爆破未遍历的位爆破
            a1 = a + i*(2**k) + j*(2**(511-k))
            b1 = b + j*(2**k) + i*(2**(511-k))
            if a1*b1 > n:
				# 当a1和b1过大
                continue
            if (a1+(2**(511-k)))*(b1+(2**(511-k))) < n:
				# 当a1和b1过小
                continue
            if ((a1*b1)%(2**(k+1))) != (n%(2**(k+1))):
				# 当a1*b1的最后k+1位（不变）与n的最后k+1位不同
                continue
			# 满足条件的(a1,b1)值，尝试继续遍历
            t(a1, b1, k+1)

# 两个素数因子有512位2进制位, 尝试可能的所有中间位
for i in xrange(2):
    t(i*(2**256), i*(2**256), 0)
    
#output:
#(13299413764048930133302138749466137829470129709829516069778014310838093114516400589047888072065037035007023741009041669893387899867083575829855377403280423L, 11954360020159164180709939019047385560179850436770100207193049651260543609501871575909448998378290922795824941066935928157032997160163537467165365731882943L)
#(11954360020159164180709939019047385560179850436770100207193049651260543609501871575909448998378290922795824941066935928157032997160163537467165365731882943L, 13299413764048930133302138749466137829470129709829516069778014310838093114516400589047888072065037035007023741009041669893387899867083575829855377403280423L)

求出 $p,q$ 值，按照RSA计算方法求出 $m$ 即为flag。

1
2
3
4
5
6
7
8
9
10
11
import gmpy2
p = 11954360020159164180709939019047385560179850436770100207193049651260543609501871575909448998378290922795824941066935928157032997160163537467165365731882943
q = 13299413764048930133302138749466137829470129709829516069778014310838093114516400589047888072065037035007023741009041669893387899867083575829855377403280423
n = p*q
fn = (p-1)*(q-1)
e = 65537
c = 103728452309804750381455306214814700768557462686461157761076359181984554990431665209165298725569861567865645228742739676539208228770740802323555281253638825837621845841771677911598039696705908004858472132222470347720085501572979109563593281375095145984000628623881592799662103680478967594601571867412886606745
d = gmpy2.invert(e,fn)
m = pow(c,d,n)
print(bytes.fromhex(hex(m)[2:]))
#flag