常用工具
分解大素数
factordb (http://www.factordb.com / API:
http://factordb.com/api?query=)yafu($p,q$相差过大或过小yafu可分解成功)
sage (
divisors(n))(小素数)Pollard’s p−1 (
python -m primefac -vs -m=p-1 xxxxxxx)(光滑数)Williams’s p+1(
python -m primefac -vs -m=p+1 xxxxxxx)(光滑数)cado-nfs
在线sage环境:https://sagecell.sagemath.org/
Openssl
解析加密密钥:
openssl rsa -pubin -text -modulus -in pub.key
生成解密密钥:
python rsatool.py -f PEM -o key.key -p 1 -q 1 -e 1
openssl rsautl -decrypt -inkey key.pem -in flag.enc -out flag
openssl rsautl -decrypt -oaep -inkey key.pem -in flag.enc -out flag (OAEP方式)
脚本生成解密密钥:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22# coding=utf-8
import math
import sys
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
n =
e =
d =
p =
q =
rsa_components = (n, e, d, p, q)
myrsa = RSA.construct(rsa_components)
private = open('private.pem', 'w')
private.write(myrsa.exportKey())
private.close()
# rsakey = RSA.importKey(myrsa.exportKey())
# rsakey = PKCS1_OAEP.new(rsakey)
# decrypted = rsakey.decrypt(c_bytes)脚本集
https://github.com/Ganapati/RsaCtfTool
1
2
3
4
5
6
7
8
9
10
11#用法一:已知公钥(自动求私钥)
$ python3 RsaCtfTool.py --publickey 公钥文件 --uncipherfile 加密文件
#用法二:已知公钥求私钥
$ python3 RsaCtfTool.py --publickey 公钥文件 --private
#用法三:密钥格式转换
#把PEM格式的公钥转换为n,e
$ python3 RsaCtfTool.py --dumpkey --key 公钥文件
#把n,e转换为PEM格式
$ python3 RsaCtfTool.py --createpub -n 782837482376192871287312987398172312837182 -e 65537https://github.com/ValarDragon/CTF-Crypto
常见类型
给p,q,e,c
1 | import gmpy2 as gp |
给n,e,dp,c
$dp\equiv d \pmod {(p-1)}$
$\because dp\cdot e\equiv d\cdot e\equiv 1 \pmod {(p-1)}$
$\therefore dp\cdot e-1=k\cdot (p-1)$
$\therefore (dp\cdot e-1)\cdot d\cdot e=k’\cdot (p-1),\quad k’=k\cdot d\cdot e \\\Leftrightarrow d\cdot e=-k’\cdot (p-1)+dp\cdot e\cdot d\cdot e\equiv 1 \pmod{\varphi(n)}\\\Leftrightarrow -k’\cdot (p-1)+dp\cdot e\equiv 1\pmod{\varphi(n)}$
$\therefore k_{1}\cdot (p-1)+dp\cdot e-1=k_{2}\cdot (p-1)\cdot (q-1)\\\Leftrightarrow (p-1)\cdot (k_{2}\cdot (q-1)-k_{1})+1=dp\cdot e$
$\because dp<p-1\quad \therefore (k_{2}\cdot (q-1)-k_{1})\in (0, e)$
$\therefore$ 遍历 $(1, e)$,当同时满足 $(dp\cdot e-1)\bmod i==0$ 和 $n\bmod((dp\cdot e-1)//i+1)==0$ 时,$N$ 成功分解。
1 | from Crypto.Util.number import * |
变种1:给 $p,e,d_p,c,b$,其中 $n=p^bq$。
Hensel lifting for Takagi’s scheme(p.189):

1
2
3
4
5
6
7
8
9
10
11
12
13
14from Crypto.Util.number import *
import gmpy2
p =
dp =
c =
b =
e =
mp1 = pow(c, dp, p)
mp = pow(c, dp - 1, p)
for i in range(1, b - 2):
x = pow(c - pow(mp1, e), 1, p**(i + 1))
y = pow(x * mp * (gmpy2.invert(e, p)), 1, p**(i + 1))
mp1 = mp1 + y
print(long_to_bytes(mp1))变种2:给 $n,e,dp_0,c,k$,其中 $dp_0$ 为 $dp$ 高 $(n\text{bits}-k)$ 位,即 $dp_0=dp>>k$。
(Coppersmith攻击,已知dp高位攻击)
$e\cdot dp \equiv e\cdot d\equiv 1 \pmod {(p-1)} \\\Leftrightarrow e \cdot dp=k(p-1)+1=kp-k+1 \\\Leftrightarrow e\cdot dp+k-1 \equiv 0 \pmod p$
$\because dp<p-1$,$\therefore k<e$
$\therefore e\cdot (dp_0<<k+x)+k-1 \equiv 0 \pmod p$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23#Sage
dp0 =
e =
n =
F.<x> = PolynomialRing(Zmod(n))
d = inverse_mod(e, n)
for k in range(1, e):
f = (secret << 200) + x + (k - 1) * d
x0 = f.small_roots(X=2 ** (200 + 1), beta=0.44, epsilon=1/32)
if len(x0) != 0:
dp = x0[0] + (secret << 200)
for i in range(2, e):
p = (e * Integer(dp) - 1 + i) // i
if n % p == 0:
break
if p < 0:
continue
else:
print('k = ',k)
print('p = ',p)
print('dp = ',dp)
break变种3:给 $n,e,dp,c$,其中 $dp$ 很小,$e$ 很大。
枚举 $dp$,因 $e\cdot dp \equiv 1 \pmod {(p-1)}$,又由费马小定理,对任意 $r$,有 $m^{e \cdot dp}\equiv m \pmod p$,即 $p \mid (m^{e \cdot dp}-m)$;
又 $p \mid n$,很大概率 $p=\gcd(m^{e \cdot dp}-m,n)$。
变种4:给 $N,e,c$,其中 $dp$ 过小。
情形1:$q<N^{0.382}$
参数 $\beta=\cfrac{q_{\text{bit}}}{N_{\text{bit}}}, \delta=\cfrac{dp_{\text{bit}}}{N_{\text{bit}}}$,满足 $3\beta < 1+\beta^2+2\delta$,可确定 $\beta$ 和 $\delta$ 的值。
构造格子维度为 $n$,格子中模数 $N$ 的最大次幂为 $m$,应满足关系
$\cfrac{m(m+1)}{2} + \cfrac{n(n-1)(2\delta+\beta)}{2}-(1-\beta)nm < 0$
确定 $\beta$ 和 $\delta$ 之后,可枚举确定 $n$ 和 $m$ 的取值(最小值),$m=(1-\beta)n$ 是一个较优的取值。
1
2
3
4
5beta =
delta =
n = round((1-2*beta-2*delta)/((1-beta)^2-2*delta-beta),6)
m = (1-beta)*n
print(m,n)构造多项式,分解多项式为 $(ax+by)$ 项,其中 $a=k,b=dp$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40# 脚本1
# Sage
def getC(Scale):
C = [[0 for __ in range(Scale)] for _ in range(Scale)]
for i in range(Scale):
for j in range(Scale):
if i == j or j == 0:
C[i][j] = 1
else:
C[i][j] = C[i-1][j-1] + C[i-1][j]
return C
def getMatrix(Scale, Mvalue, N, E, Del, Bet):
M = [[0 for __ in range(Scale)] for _ in range(Scale)]
C = getC(Scale)
X, Y = int(pow(N,Del)*(Scale+1)//2), int(pow(N,(Del+Bet))*(Scale+1)//2)
for i in range(Scale):
for j in range(Scale):
M[i][j] = N**max(Mvalue-i,0)*E**(max(i-j,0))*X**(Scale-1-j)*Y**j*C[i][j]*(-1)**j
return M
N =
E =
delta = 0.01
beta = 0.37
Scale = 35
Mvalue = 22
M = getMatrix(Scale,Mvalue,N,E,delta,beta)
M = matrix(ZZ,M)
A = M.LLL()[0]
p = []
X = int(pow(N,delta)*(Scale+1)//2)
Y = int(pow(N,(delta+beta))*(Scale+1)//2)
for i in range(Scale):
p.append(A[i]//(X**(Scale-1-i)*Y**i))
PR.<x,y> = PolynomialRing(ZZ)
f = 0
for i in range(Scale):
f += p[i]*x^(Scale-1-i)*y^i
print(f.factor())1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36# 脚本2
# Sage
N =
e =
n = 12
beta = 0.36
delta = 0.02
X = int(N ** delta*(n+1)/2)
Y = int(N ** (delta + beta)*(n+1)/2)
def C(a,b):
ret=1
for i in range(b):
ret *= (a-i)
ret /= (b-i)
return ret
def get_Matrix(n,m):
MM=[[0 for __ in range(n)] for _ in range(n)]
for j in range(n):
pN = max(0,m-j)
for i in range(j+1):
MM[j][i] = pow(N,pN)*pow(X,n-i-1)*pow(Y,i)*pow(e,j-i)*C(j,i)*pow(-1,i)
MM = Matrix(ZZ,MM)
return MM
M = get_Matrix(n,n//2+1)
L = M.LLL()[0]
x,y = var('x'),var('y')
f = 0
for i in range(n):
f += x**(n-i-1) * y**i * (L[i] // pow(X,n-i-1) // pow(Y,i))
print(f.factor())参考:
Cryptanalysis of Unbalanced RSA with Small CRT-Exponent
https://hash-hash.github.io/2022/05/14/Unbalanced-RSA-with-Small-CRT-Exponent/#An-Approach-Modulo-e
NSSCTF Round#3 - Secure_in_N
情形2:$q<N^{0.468}$
参数 $\beta=\cfrac{q_{\text{bit}}}{N_{\text{bit}}}, \delta=\cfrac{dp_{\text{bit}}}{N_{\text{bit}}},\alpha=\cfrac{e_{\text{bit}}}{N_{\text{bit}}}$,
变量上界 $X=2N^{\alpha+\beta+\delta-1},Y=N^{\beta},Z=2N^{1-\beta}$ ,对于变量 $m$ 需充分大。
$\tau=\cfrac{(1-\beta)^2-\delta}{2\beta(1-\beta)},\sigma=\cfrac{1-\beta-\delta}{2(1-\beta)},t=\tau m,s=\sigma m$
整数域上有根 $(x,y,z)=(x_0,p,q)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117from copy import deepcopy
# https://www.iacr.org/archive/pkc2006/39580001/39580001.pdf
# Author: ZM__________J, To1in
N =
e =
alpha = log(e, N)
beta =
delta =
P.<x,y,z>=PolynomialRing(ZZ)
X = ceil(2 * N^(alpha + beta + delta - 1))
Y = ceil(2 * N^beta)
Z = ceil(2 * N^(1 - beta))
def f(x,y):
return x*(N-y)+N
def trans(f):
my_tuples = f.exponents(as_ETuples=False)
g = 0
for my_tuple in my_tuples:
exponent = list(my_tuple)
mon = x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]
tmp = f.monomial_coefficient(mon)
my_minus = min(exponent[1], exponent[2])
exponent[1] -= my_minus
exponent[2] -= my_minus
tmp *= N^my_minus
tmp *= x ^ exponent[0] * y ^ exponent[1] * z ^ exponent[2]
g += tmp
return g
m = 5 # need to be adjusted according to different situations
tau = ((1 - beta)^2 - delta) / (2 * beta * (1 - beta))
sigma = (1 - beta - delta) / (2 * (1 - beta))
print(sigma * m)
print(tau * m)
s = ceil(sigma * m)
t = ceil(tau * m)
my_polynomials = []
for i in range(m+1):
for j in range(m-i+1):
g_ij = trans(e^(m-i) * x^j * z^s * f(x, y)^i)
my_polynomials.append(g_ij)
for i in range(m+1):
for j in range(1, t+1):
h_ij = trans(e^(m-i) * y^j * z^s * f(x, y)^i)
my_polynomials.append(h_ij)
known_set = set()
new_polynomials = []
my_monomials = []
# construct partial order
while len(my_polynomials) > 0:
for i in range(len(my_polynomials)):
f = my_polynomials[i]
current_monomial_set = set(x^tx * y^ty * z^tz for tx, ty, tz in f.exponents(as_ETuples=False))
delta_set = current_monomial_set - known_set
if len(delta_set) == 1:
new_monomial = list(delta_set)[0]
my_monomials.append(new_monomial)
known_set |= current_monomial_set
new_polynomials.append(f)
my_polynomials.pop(i)
break
else:
raise Exception('GG')
my_polynomials = deepcopy(new_polynomials)
nrows = len(my_polynomials)
ncols = len(my_monomials)
L = [[0 for j in range(ncols)] for i in range(nrows)]
for i in range(nrows):
g_scale = my_polynomials[i](X * x, Y * y, Z * z)
for j in range(ncols):
L[i][j] = g_scale.monomial_coefficient(my_monomials[j])
# remove N^j
for i in range(nrows):
Lii = L[i][i]
N_Power = 1
while (Lii % N == 0):
N_Power *= N
Lii //= N
L[i][i] = Lii
for j in range(ncols):
if (j != i):
L[i][j] = (L[i][j] * inverse_mod(N_Power, e^m))
L = Matrix(ZZ, L)
nrows = L.nrows()
L = L.LLL()
# Recover poly
reduced_polynomials = []
for i in range(nrows):
g_l = 0
for j in range(ncols):
g_l += L[i][j] // my_monomials[j](X, Y, Z) * my_monomials[j]
reduced_polynomials.append(g_l)
# eliminate z
my_ideal_list = [y * z - N] + reduced_polynomials
# Variety
my_ideal_list = [Hi.change_ring(QQ) for Hi in my_ideal_list]
for i in range(len(my_ideal_list),3,-1):
print(i)
V = Ideal(my_ideal_list[:i]).variety(ring=ZZ)
print(V)参考:
给p,q,dp,dq,c
$dp=d \bmod (p-1)$,$dq=d \bmod (q-1)$
$\because d=k_{1}(p-1)+dp=k_{2}(q-1)+dq\\\Leftrightarrow k_{1}(p-1)=(dq-dp)+k_{2}(q-1)\\\Leftrightarrow k_{1}\frac{p-1}{\gcd(p-1,q-1)}=\frac{dq-dp}{\gcd(p-1,q-1)}+k_{2}\frac{q-1}{\gcd(p-1,q-1)}\\\Rightarrow k_{1}\frac{p-1}{\gcd(p-1,q-1)}\equiv\frac{dq-dp}{\gcd(p-1,q-1)} \pmod {\frac{q-1}{\gcd(p-1,q-1)}}\\\Leftrightarrow k_{1}\equiv \text{inv}(\frac{p-1}{\gcd(p-1,q-1)},\frac{q-1}{\gcd(p-1,q-1)})\cdot \frac{dq-dp}{\gcd(p-1,q-1)} \pmod {\frac{q-1}{\gcd(p-1,q-1)}}$
将 $k_{1}=k_{3}\frac{q-1}{\gcd(p-1,q-1)}+\text{inv}(\frac{p-1}{\gcd(p-1,q-1)},\frac{q-1}{\gcd(p-1,q-1)})\cdot \frac{dq-dp}{\gcd(p-1,q-1)}$
代入 $d=k_{1}(p-1)+dp$
$d=k_{3}\frac{(p-1)(q-1)}{\gcd(p-1,q-1)}+\text{inv}(\frac{p-1}{\gcd(p-1,q-1)},\frac{q-1}{\gcd(p-1,q-1)})\cdot \frac{(dq-dp)(p-1)}{\gcd(p-1,q-1)}+dp\\\Rightarrow d\equiv \text{inv}(\frac{p-1}{\gcd(p-1,q-1)},\frac{q-1}{\gcd(p-1,q-1)})\cdot \frac{(dq-dp)(p-1)}{\gcd(p-1,q-1)}+dp \pmod{\frac{(p-1)(q-1)}{\gcd(p-1,q-1)}}$
1 | from Crypto.Util.number import * |
给e,d,n
计算 $k=ed-1$,选择一个随机数 $g,g \in (1,N)$。
$k$ 为偶数,故 $k=2^tr$,其中 $r$ 为奇数且 $t \ge 1$,然后计算 $x = g^{\frac{k}{2}},g^{\frac{k}{4}},\cdots,g^{\frac{k}{2^t}} \pmod N$ 直到 $x \gt 1$ 且 $y=\gcd(x-1,N) \gt 1$。
如果这样的 $y$ 存在,则其中的因子 $p=y,q=\cfrac{N}{y}$;如这样的 $y$ 不存在,则重新生成随机数 $g$。
1 | import random |
1 | import random |
低解密指数攻击/低私钥指数攻击(e长度较大,d小,Wiener Attack)
适用情况:已知 $N,e$,且 $e$ 过大或过小。
$\varphi(n) = (p-1)(q-1)=pq - (p + q) + 1=N - (p + q) + 1$
$\because p, q$ 非常大,$\therefore\,pq\gg p+q$, $\therefore\varphi(n)\approx N$
$\because ed\equiv1\,mod\,\varphi(n)$,$\therefore ed-1=k\varphi(n)$,这个式子两边同除 $d\varphi(n)$ 可得:
$\cfrac{e}{\varphi(n)}-\cfrac{k}{d}=\cfrac{1}{d\varphi(n)}$
$\because \varphi(n)\approx N$,$\therefore \cfrac{e}{N}-\cfrac{k}{d}=\cfrac{1}{d\varphi(n)}$,同样 $d\varphi(n)$ 是一个很大的数,所以 $\cfrac{e}{N}$ 略大于 $\cfrac{k}{d}$
因为 $e$ 和 $N$ 是知道的,所以计算出 $\cfrac{e}{N}$ 后,比它略小的 $\cfrac{k}{d}$ ,可以通过计算 $\cfrac{e}{N}$ 的连分数展开,依次算出这个分数每一个渐进分数,由于 $\cfrac{e}{N}$ 略大于 $\cfrac{k}{d}$,Wiener 证明了,该攻击能精确的覆盖 $\cfrac{k}{d}$。
在 $e$ 过大或过小的情况下,可使用算法从 $e$ 中快速推断出 $d$ 的值。可以解决 $q<p<2q,d<\cfrac{1}{3}N^{\frac{1}{4}}$ 的问题。
RSAWienerHacker工具:https://github.com/pablocelayes/rsa-wiener-attack
1 | #脚本1 |
1 | #脚本2 |
1 | #脚本3 |
变种1:$\cfrac{N_1}{N_2}<\cfrac{q_1}{q_2}<1$
Paper: https://eprint.iacr.org/2015/399.pdf
尝试对 $\cfrac{N_1}{N_2}$ 进行连分数展开并求其各项渐进分数,记为 $\cfrac{t_i}{s_i}$ 并验证 $N_1\% {t_k}==0$ 是否成立,如果成立,那么 $q_1=t_k,q_2=s_k$。
连分数逼近:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def transform(x,y): #使用辗转相除将分数x/y转为连分数的形式
res=[]
while y:
res.append(x//y)
x,y=y,x%y
return res
def continued_fraction(sub_res):
numerator,denominator=1,0
for i in sub_res[::-1]: #从sublist的后面往前循环
denominator,numerator=numerator,i*numerator+denominator
return denominator,numerator #得到渐进分数的分母和分子,并返回
#求解每个渐进分数
def sub_fraction(x,y):
res=transform(x,y)
res=list(map(continued_fraction,(res[0:i] for i in range(1,len(res))))) #将连分数的结果逐一截取以求渐进分数
return res
def wienerAttack(n1,n2):
for (q2,q1) in sub_fraction(n1,n2): #用一个for循环来注意试探n1/n2的连续函数的渐进分数,直到找到一个满足条件的渐进分数
if q1==0: #可能会出现连分数的第一个为0的情况,排除
continue
if n1%q1==0 and q1!=1: #成立条件
return (q1,q2)
print("该方法不适用")
N1=
N2=
print(wienerAttack(N1,N2))变种2:$Ax \equiv y \pmod P$,即 $Ax-kP=y$ 或 $Ax+kP=y$
Wiener’s:
$\Big\vert \cfrac{A}{P}-\cfrac{k}{x}\Big\vert \le \cfrac{1}{2x^2}$,连分数方法,用 $\cfrac{A}{P}$ 逼近求出 $\cfrac{k}{x}$,进而解出 $y$。
Lattice:
$(x,k)\begin{bmatrix}1&A\\0&P\ \end{bmatrix} = (x,y)$,记为 $vM=w$,$w$ 有很大概率为 $M$ 里的最短向量,使用LLL算法求出最短向量,即解出 $w’=(x,y)$。
变种3:$N=p^2q$,$q \lt p \lt2q$,$d=N^\beta$
可用 $\cfrac{e}{N-(2N^\frac{2}{3}-N^\frac{1}{3})}$ 逼近 $\cfrac{k}{d}$。
参考:New Attacks on RSA with Modulus N = p^2q Using Continued Fractions
低加密指数广播攻击(Hastad攻击)
适用情况: $n,c$ 不同,$m,e$ 相同。一般会是 $e=k$,然后给 $k$ 组数据。
如果一个用户使用同一个加密指数 e 加密了同一个密文,并发送给了其他 e 个用户。那么就会产生广播攻击。这一攻击由 Håstad 提出。
使用不同的模数 $n$,相同的公钥指数 $e$ 加密相同的信息,就会得到多个 $m^e \equiv c_i \pmod {n_i}$,将 $m^e$ 视为一个整体 $M$,这就是典型的中国剩余定理适用情况。容易求得 $m^e$ 的值,当 $e$ 较小时直接开 $e$ 方即可,可使用gmpy2.iroot(M,e) 方法。
更一般情况($k$ 组数据的 $N$ 不同)见15。
1 | #sage |
1 | #sage |
共模攻击(n,m相同,c,e不同)
当$n$不变的情况下,知道$n,e_1,e_2,c_1,c_2$可以在不知道$d_1,d_2$的情况下,解出$m$。
首先假设$e_1,e_2$互质,
即 $\gcd(e_1,e_2)=1$
此时则有 $e_1s_1+e_2s_2 = 1$
式中,$s_1,s_2$皆为整数,但是一正一负。
通过扩展欧几里德算法,我们可以得到该式子的一组解$(s_1,s_2)$,假设$s_1$为正数,$s_2$为负数。
因为 $c_1 = m^{e_1}\bmod n, c_2 = m^{e_2}\bmod n$
所以 $(c_1^{s_1}c_2^{s_2})\bmod n = ((m^{e_1}\bmod n)^{s_1}(m^{e_2}\bmod n)^{s_2})\bmod n$
根据模运算性质,可以化简为 $(c_1^{s_1}c_2^{s_2})\bmod n = ((m^{e_1})^{s_1}(m^{e_2})^{s_2})\bmod n$
即 $(c_1^{s_1}c_2^{s_2})\bmod n = (m^{e_1s_1+e_2s_2})\bmod n$
又前面提到 $e_1s_1+e_2s_2 = 1$
所以 $(c_1^{s_1}c_2^{s_2})\bmod n = m\bmod n$
即 $c_1^{s_1}c_2^{s_2}= m$
1 | import gmpy2 as gp |
e,m相同,多个n中存在两个n有GCD(模不互素)
适用情况:存在两个或更多模数 ,且 $\gcd(n_1,n_2)\ne 1$ 。
多个模数 $n$ 共用质数,则可以很容易利用欧几里得算法求得他们的质因数之一 $\gcd(n_1,n_2)$,然后这个最大公约数可用于分解模数分别得到对应的 $p$ 和 $q$,即可进行解密。
1 | import gmpy2 as gp |
Rabin加密
适用情况:$e=2$ 。
一般先通过其他方法分解得到 $p,q$,然后解密。
函数返回四个数,这其中只有一个是我们想要的明文,需要通过其他方式验证。
1 | import gmpy2 |
Boneh and Durfee attack
$e$ 非常大接近于$N$,即 $d$ 较小时。与低解密指数攻击类似,比低解密指数攻击(Wiener Attack)更强,可以解决$\cfrac{1}{3}N^{\frac{1}{4}} \leq d \leq N^{0.292}$的问题。
$\because ed=k \varphi +1$
$\therefore k \varphi+1 \equiv 0 \pmod e \Rightarrow k(N+1-p-q)+1 \equiv 0 \pmod e \Rightarrow 2k(\frac{N+1}{2}+\frac{-p-q}{2}) \equiv 0 \pmod e$
设 $A=\frac{N+1}{2},y=\frac{-p-q}{2},x=2k$,有 $f(k,y)=1+x\cdot(A+y)$
如果在模 $e$ 下解得该方程的根 $x,y$,由 $ed=1+x\cdot(A+y)$ 可以得到 $d$。
变种1:$e$ 很大,$dp$ 很小,且 $d>2N^{\beta}$。
May’s Attack
假设 $e<\varphi(N),q \le N^{\beta},\beta \le \frac{1}{2}$,因 $ed_p \equiv 1 \pmod {p-1}$,有 $ed_p=1+k(p-1)$,
对于 $k \in \mathbb{N}$,有 $ed_p=(k-1)(p-1)+p$,即 $ed_pq=(k-1)(N-q)+N$。
设 $x,y$ 为参数,则多项式 $f(x,y)=x(N-y)+N$ 在模 $e$ 下存在根 $(x_0,y_0)=(k-1,q)$,用coppersmith attack可解。
光滑数
p-1 光滑
Pollard’s p-1分解算法。
如果一个整数的所有素因子都不大于 $B$,我们称这个数为 $B$-Smooth 数。
设 $p-1$ 是 $B$-Smooth 的,可设 $p-1=p_1p_2 \cdots p_n(\forall 1 \leq i \leq n,p_i \leq B)$,
若 $p_1,p_2, \cdots ,p_n$ 两两不同,则 $p_1p_2 \cdots p_n \mid B! \Rightarrow (p-1) \mid B! \Rightarrow B!=k(p-1)$。
因此 $a^{B!} \equiv a^{k(p-1)} \equiv 1 \pmod p$,假设 $N=pq$,计算 $\gcd(a^{B!}-1,N)$,只要结果大于 $0$ 小于 $N$,那么结果就为 $p$。
1 | from gmpy2 import * |
p+1 光滑
William’s p+1分解算法。
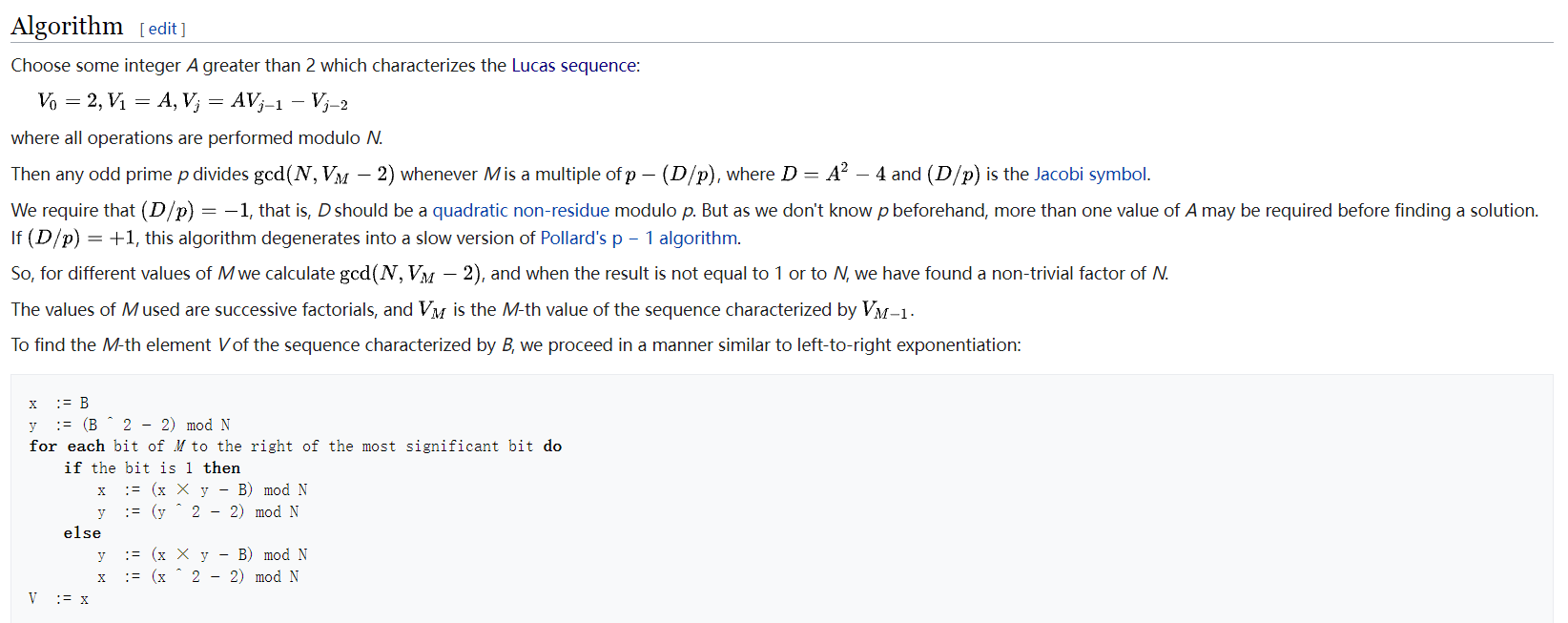
1 | def mlucas(v, a, n): |
Coppersmith定理指出在一个 $e$ 阶的 $\bmod n$ 多项式 $f(x)$ 中,如果有一个根小于 $n^{\frac{1}{e}}$,就可以运用一个 $O(\log n)$ 的算法求出这些根。
Coppersmith攻击(已知p的高位攻击)
知道 $p$ 的高位为 $p$ 的位数的约$\frac12$时即可。
1 | #Sage |
Coppersmith攻击(已知m的高位攻击)
这里我们假设我们首先加密了消息 $m$,如下
$C\equiv m^e \bmod N$
并且我们假设我们知道消息 $m$ 的很大的一部分 $m_0$,即 $m=m_0+x$,但是我们不知道 $x$。那么我们就有可能通过该方法进行恢复消息。这里我们不知道的 $x$ 其实就是多项式的根,需要满足 Coppersmith 的约束。
可以参考 https://github.com/mimoo/RSA-and-LLL-attacks 。
$e$ 足够小,且部分明文泄露时,可以采用Coppersmith单变量模等式的攻击,如下:
$c=m^{e}\bmod n=(mbar+x_{0})^{e}\bmod n$,其中 $mbar = (m >> k\text{bits}) << k\text{bits}$
当 $\vert x_{0}\vert\leq N^{\frac{1}{e}}$ 时,可以在 $\log N$ 和 $e$ 的多项式时间内求出 $x_0$。
1 | #Sage |
Coppersmith攻击(已知d的低位攻击)
如果知道 $d$ 的低位,低位约为 $n$ 的位数的 $\frac14$ ($\frac{n.n\text{bits}()}{4}$)就可以恢复 $d$。
1 | #Sage |
变种1:$n=p\cdot q\cdot r$,已知 $n,p,d=\text{inv}(e,\varphi(n)),e,c$
$k(p-1)\rightarrow k’,qr\rightarrow n’,q+r\rightarrow s$
$ed_{0}\equiv 1+k’(n’-s+1) \pmod {2^{d_{0}.n\text{bits}()}}\quad (1)$
$q^{2}-sq+n’\equiv 0 \pmod {2^{d_{0}.n\text{bits}()}}\quad (2)$
联立可得,$(ed_{0}-1-k’n’-k’)q+k’q^{2}+k’n’\equiv 0 \pmod {2^{d_{0}.n\text{bits}()}}$
即求解同余方程可得 $q$ 的低 $size(d0)$ 位,本来是个partial d的coppersmith问题,但因为step1求解同余方程后得到的 $q$ 已是完整的 $q$,所以无需后续的coppersmith。
参考:Dragon CTF 2019 - RSA Chained
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22#Sage
def find_p(d0, kbits, e, n, p):
X = var('X')
for k in range(1, e + 1):
k_dot = k * (p - 1)
results = solve_mod([e * d0 * X - k_dot * X * (n - X + 1) + k_dot * n == X], 2^kbits)
for x in results:
q = ZZ(x[0])
if n % q == 0:
return q
return None
n = ... # q * r
p =
c =
d0 =
e =
kbits = d0.nbits()
q = find_p(d0, kbits, e, n, p)
phi = (p - 1) * (q - 1) * (n // q - 1)
d = inverse_mod(e, phi)
print(bytes.fromhex(hex(pow(c, d, p * n))[2:]))
Coppersmith攻击(已知N一个因子的高位,部分p)
当我们知道一个公钥中模数 $N$ 的一个因子的较高位时,我们就有一定几率来分解 $N$。
参考 https://github.com/mimoo/RSA-and-LLL-attacks 。
关注下面的代码:
1 | beta = 0.5 |
其中,
- 必须满足 $q\ge N^{beta}$,所以这里给出了 $beta=0.5$,显然两个因数中必然有一个是大于的。
- XX 是 $f(x)=q′+x$ 在模 $q$ 意义下的根的上界,自然我们可以选择调整它,这里其实也表明了我们已知的 $q′$ 与因数 $q$ 之间可能的差距。
1 | #Sage |
注:
sage的small_root传参X不能过大,需自行判断阈值并调整(如果X过大,即使存在X内的解,也无法求出);
比如 $p$ 的低位泄露时因为不确定缺失高位的具体比特数,所以要在 $2^{\frac{n.n\text{bits}()}{2}−k\text{bits}}$ 附近作X的阈值估计;
无法确定拿到的 $p$ 是否大于 $q$,所以对 $\beta=0.5$ 进行调整至 $0.4$。
Coppersmith’s Short-pad Attack & Related Message Attack(Franklin-Reiter攻击)
目前在大部分消息加密之前都会进行 padding,但是如果 padding 的长度过短($m \in (0,\lfloor\frac{n.n\text{bits}()}{e^2}\rfloor]$),也有可能被很容易地攻击。
这里所谓 padding 过短,其实就是对应的多项式的根会过小。
当 Alice 使用同一公钥对两个具有某种线性关系的消息 $M_1$ 与 $M_2$ 进行加密,并将加密后的消息 $C_1$,$C_2$ 发送给了 Bob 时,我们就可能可以获得对应的消息 $M_1$ 与 $M_2$ 。这里我们假设模数为 $N$,两者之间的线性关系如下:
$M_1 \equiv f(M_2) \bmod N$
其中 $f$ 为一个线性函数,比如说 $f=ax+b$。
在具有较小错误概率下的情况下,其复杂度为 $O(e\log^2N)$。
这一攻击由 Franklin与Reiter 提出。
1 | #脚本1 |
1 | #脚本2 |
变种1:$e$ 较大。使用Half GCD降低时间复杂度。
变种2: $c_i=(a_im+b_i)^e \pmod {n_i}$
用CRT计算系数 $T_i$ 使得 $T_i \equiv 1 \pmod{n_i},T_i \equiv 0 \pmod{n_{j \neq i}}$,
则可建立多项式为 $f(x) = \sum_{i} T_i [ (a_i x + b_i)^e - c_i]$,符合 $f(m) \equiv 0 \pmod{n_i}$,
故 $m$ 是 $f(m) \equiv 0 \pmod N$ 的一个根,其中 $N= \prod_i n_i$。
如果 $m < \left (\prod_i n_i \right)^{1/e} = M^{1/\deg{f(x)}}$,可以使用coppersmith找出 $m$。
参考:
RSA Hastad Attack with non-linear padding and different public keys(带非线性padding和不同公钥的广播攻击)
适用情况:$m$ 经 $k$ 次非线性padding处理后,分别用 $k$ 组 $(N_i,e_i)$ 加密后得 $k$ 组 $c_i$。
参考:2020年羊城杯 - Invitation
1 | #Sage |
选择明/密文攻击
选择明文攻击
适用情况:对输入的任意明文服务器返回 RSA 加密结果,可以通过选择明文攻击来获取 $n$。
首先发送 $2$,让服务器进行加密,返回 $c_2=2^e \bmod n$;
继续发送 $2^2$,让服务器进行加密,返回 $c_4=4^e \bmod n$;
不妨设 $2^e=a+bn$,有 $c_2=(a+bn) \bmod n=a$,$c_4=(a^2+2abn+b^2n^2) \bmod n = a^2 \bmod n$,
所以 $c_2^2$ 和 $c_4$ 模 $n$ 同余,即 $c_2^2-c_4=kn$,同理 $c_2^3-c_8=k’n$,
一般来说 $a^2$ 比 $n$ 大,所以 $k \neq 0$。
同理还可以构造更多的例子取他们的公因数,来更加确定地找 $n$。
1 | import gmpy2 |
选择密文攻击
适用情况:可以构造任意密文并获得对应明文,通过选择密文攻击获得特定的明文。
假设服务器创建了密文 $c=m^e \bmod n$,并且把 $c$ 发送给用户,用户可以发送任意密文服务器返回解密后的明文,可以通过以下方法求出 $m$:
- 选择任意的 $x$ 与 $n$ 互素;
- 计算 $y=cx^e \bmod n$;
- 由于可以进行选择密文攻击,可以求得 $y$ 对应的解密结果 $z=y^d$;
- 则 $z=y^d=(cx^e)^d=c^dx=mx \bmod n$,由于 $x$ 与 $n$ 互素,容易求得相应逆元,进而可以得到 $m$。
1 | from Crypto.Util.number import * |
Parity Oracle Attack
LSB Oracle Attack(Least Significant Bit Oracle Attack )
适用情况:可以选择密文并泄露明文的最低位(奇偶性)。
服务器会对一个给定的密文进行解密,并且会检查解密的明文的奇偶性,并根据奇偶性返回相应的值,比如1表示奇数,0表示偶数。那么给定一个加密后的密文,只需要 $\log_2n$ 次就可以知道这个密文对应的明文消息。
假设 $c=m^e \bmod n$,第一次时,构造密文 $c \cdot 2^e \bmod n=(2m)^e \bmod n$,服务器解密后得到 $2m \bmod n$。
这里:
- $2m$ 是偶数,它的幂次也是偶数;
- $n$ 是奇数,因为它是由两个大素数相乘得到。
那么:
- 服务器返回奇数,即 $2m \bmod n$ 为奇数,则说明 $2m>n$,且减去了奇数个 $n$,又因为 $2m<2n$,因此减去了一个 $n$,即 $\frac{n}{2}\leq m \lt n$;
- 服务器返回偶数,则 $2m<n$,即 $0 \leq m \lt \frac{n}{2}$。
第二次时,构造密文 $c \cdot 4^e \bmod n$,服务器解密后得到 $4m \bmod n$,判断其奇偶性可以知道 $m$ 和 $\frac{n}{4}$ 的大小关系。
以此类推,第 $i$ 次时,构造密文 $c \cdot 2^{ie} \bmod n$,服务器解密后得到 $2^im \bmod n$,判断其奇偶性可以知道 $m$ 和 $\frac{n}{2^i}$ 的大小关系。
所以我们就有了一个二分算法,可以在 $\log_2n$ 次内将 $m$ 的范围逼近到一个足够狭窄的空间。
假设服务器返回 b,那么可以归纳为:
1 | L = 0 |
由于此处有大量整除运算,所以最好用 decimal 库进行精确计算,否则最后结果很可能会出错。decimal.getcontext().prec 用来设定精度。
1 | from Crypto.Util.number import * |
更多信息可参考:RSA Least-Significant-Bit Oracle Attack 和 RSA least significant bit oracle attack 。
1 | import decimal |
MSB Oracle Attack(Most Significant Bit Oracle Attack )
适用情况:可以选择密文并泄露明文的最高位(奇偶性)。
假设远程提供一个解密服务,但是只返回明文的最高字节,并且明文的形式是64字节,高位用 \x00 填充。
将加密的内容拿去解密会得到 $m$,但是回显最高位是 \x00,构造密文 $c \cdot 2^e$,解密会得到 $2m \bmod n$,
不断构造密文 $c \cdot 2^{ie}$,当最高位不是 \x00 时,记录下值为 $x$,则说明 $mx>2^{\text{kbit}}$,
然后再相应缩小 $x$ ,可以利用二分法,比如当第一次拿到 $mx>2^{\text{kbit}}$,那么有 $m(\frac{x}{2})<2^{\text{kbit}}$,因此新的 $x’$ 必定满足 $\frac{x}{2} \lt x’ \lt x$,接着尝试 $\frac{x+\frac{x}{2}}{2}$ 就好。
最终可以找到一个 $X$,满足 $mX \lt 2^{\text{kbit}}$ 且 $m(X+1) \gt 2^{\text{kbit}}$,由于是整除,所以会有误差,最后的 $m$ 在 $\frac{2^{\text{kbit}}}{x}$ 附近。
参考:Pwnhub - pkcs4
Byte Oracle Attack
适用情况:可以选择密文并泄露最后一个字节。
服务器会对一个给定的密文进行解密,并且会给出明文的最后一个字节。那么给定一个加密后的密文,只需要 $\log_{256}n$ 次就可以知道这个密文对应的明文消息。
这是 RSA Parity Oracle 的扩展,既然可以泄露出最后一个字节,那么按道理获取密文对应明文的次数应该可以减少。
假设 $c=m^e \bmod n$,第一次时,构造密文 $c \cdot 256^e \bmod n=(256m)^e \bmod n$,服务器解密后得到 $256m \bmod n$。
这里:
- $256m$ 是偶数,它的幂次也是偶数;
- $n$ 是奇数,因为它是由两个大素数相乘得到。
由于 $m=c^d \bmod n$,所以 $m \lt n$,那么:$256m \bmod n=256m-kn$,$(k<256)$,
而且对于两个不同的 $k_1,k_2$,有:$(256m-k_1n) \bmod 256 \neq (256m-k_2n) \bmod 256$,
同时 $256m-kn$ 的最后一个字节其实就是 $-kn$ 在模 $256$ 的情况下获取的。
那么,可以首先枚举出 $0 \sim 255$ 情况下的最后一个字节,构造一个 $k$ 和最后一个字节的映射表 $\text{M}$。
当服务器返回最后一个字节,可以根据上述构造的映射表 $\text{M}$ 得知 $k$,即减去了 $k$ 个 $n$,即 $kn \leq 256m \leq (k+1)n$。
以此类推,第 $i$ 次时,构造密文 $c \cdot 256^{ie} \bmod n$,服务器解密后得到 $256^im \bmod n = 256^im-kn$,即:
$kn \leq 256^im \leq (k+1)n$, $\frac{kn}{256^i} \leq m \leq \frac{(k+1)n}{256^i}$。
那么,可以设初始范围为:$\frac{M}{n} \in [L_0,R_0],(L_0=0,R_0=1)$,
第 $i$ 次迭代后:$L_i=L_{i-1}+\frac{k_i}{256^i},R_i=R_{i-1}+\frac{k_i+1}{256^i}$。
最后一个问题是迭代的次数,由于明文的最后一个字节可以直接由服务器解密得到,那么只需要限定 $m$ 的范围至 $m_{\text{max}}-m_{\text{min}} \lt 256$,即 $n(R_i-L_i)= \frac{n}{256^i} \lt 256$。
例如,假设 $n \lt 2^{1024}$,由上式可得 $i \gt 128$。
一般对于这样的 Oracle,最多需要 $\log_{2^{\text{bits}}}n$ 次迭代即可确定明文,其中 bits 为泄露的明文 bit 数。RSA Parity Oracle 为 1,RSA Byte Oracle 为 8。
假设服务器返回了 b,那么可以归纳为:
1 | L = 0 |
如果不知道 $e$ 但服务器提供任意明文加密服务,可以让服务器加密 $256$,得到 $256^e \bmod n$。
由于有大量除法运算,为保证精度,将中间过程用 Fraction 库保存为分数。
最后一字节的数据不准确要减掉,从服务器返回精确的最后一字节数据。
其实只要求出 L 下限即可,无需求出 R 上限。
1 | from Crypto.Util.number import * |
Common Private Exponent(共私钥指数攻击,d相同)
加密用同样的私钥并且私钥比较短,从而导致了加密系统被破解。
假定:
$\begin{cases} e_1d=1+k_1\varphi(N_1) \newline e_2d=1+k_2\varphi(N_2) \newline {\vdots} \newline e_rd=1+k_r\varphi(N_r) \end{cases}$
其中,$N_1 \lt N_2 \lt \cdots \lt N_r \lt 2N_1$。
构造格:
$B_r=\begin{bmatrix}{M}&{e_1}&{e_2}&{\cdots}&{e_{r}}\newline
{0}&{-N_1}&{0}&{\cdots}&{0}\newline{0}&{0}&{-N_2}&{\cdots}&{0}\newline{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}\newline{0}&{0}&{0}&{\cdots}&{-N_r}\newline\end{bmatrix}$
其中 $M=\lfloor N_r^{\frac{1}{2}} \rfloor$。
再利用LLL算法进行规约得到 $\vert b_1\vert=Md$,则 $d=\cfrac{\vert b_1 \vert}{M}$,从而解密密文得到明文。
使用条件:
$d \lt N_r^{\delta_r},\delta_r \lt \cfrac{1}{2}-\cfrac{1}{2(r+1)}-\log_{N_r}{(6)}$
参考:
Lattice Based Attack on Common Private Exponent RSA
SCTF 2020 - RSA
1 | ###Sage### |
多组低解密指数攻击
适用情况:2-4组 $e$,且 $d$ 较小
给定2组
$g=\gcd(p-1,q-1),\lambda(n)=\frac{\varphi(n)}{g},s=1-p-q$
且有 $ed-k\lambda(n)=1$,得到 $edg-kn=g+ks\quad (1)$
设 $e_1$ 对应 $k_1$,$e_2$ 对应 $k_2$,则有 $k_{2}d_{1}e{1}-k_{1}d_{2}e_{2}=k_{2}-k_{1}\quad (2)$
由(1)(2)有:
$\left\{ \begin{matrix} e_{1}d_{1}g-k_{1}n=g+k_{1}s \newline k_{2}d_{1}e{1}-k_{1}d_{2}e_{2}=k_{2}-k_{1} \newline e_{1}e_{2}d_{1}d_{2}g_{2}-e_{1}d_{1}gk_{2}n-e_{2}d_{2}gk_{1}n+k_{1}k_{2}n^{2}=(g+k_{1}s)(g+k_{2}s) \end{matrix} \right.$
上述等式组也可表示为
$bL_2 =[k_{1}k_{2},k_{2}d_{1}g,k_{1}d_{2}g,d_{1}d_{2}g^{2}]\cdot\left[ \begin{matrix} n & -M_{1}n & 0 & n^{2} \newline 0 & M_{1}e_{1} & M_{2}e_{1} & -e_{1}n \newline 0 & 0 & -M_{2}e_{2} & -e_{2}n \newline 0 & 0 & 0 & e_{1}e_{2} \end{matrix} \right] =[k_{1}k_{2}n,M_{1}k_{2}(g+k_{1}s),M_{2}g(k_{2}-k_{1}),(g+k_{1}s)(g+k_{2}s)]$
(其中 $M_{1}=n^{1/2},M_{2}=n^{1+\alpha_{2}},d\approx n^{\alpha_{2}}$)
对部分参数进行上界估计,k上界近似于 $d\approx N^{\alpha_{2}}$, $|s|$ 上界 $\approx N^{1/2}$,$g$ 一般相对极小
因此上面的矩阵表示 $BA=C$ 中,$C$ 的每个元的size都近似 $n^{1+2\alpha_{2}}$,所以 $|C|\approx 2\cdot n^{1+2\alpha_{2}}$
$B$ 作为格基的格中,最短向量由Minkowski Bounds知 $\approx \sqrt{4}\det(B)^{1/4}\approx 2\cdot n^{(13/2+\alpha_{2})/4}$
因此只要满足 $n^{1+2\alpha_{2}}<n^{(13/2+\alpha_{2})/4}$ 即可将问题转化为SVP($\alpha_{2}<\frac{5}{14}$)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28from sage.all import *
import gmpy2
N =
e1 =
e2 =
c =
for i in range(1000):
alpha2 = i/1000
M1 = int(gmpy2.mpz(N)**0.5)
M2 = int( gmpy2.mpz(N)**(1+alpha2) )
D = diagonal_matrix(ZZ, [N, M1, M2, 1])
B = Matrix(ZZ, [ [1, -N, 0, N**2],
[0, e1, -e1, -e1*N],
[0, 0, e2, -e2*N],
[0, 0, 0, e1*e2] ]) * D
L = B.LLL()
v = Matrix(ZZ, L[0])
x = v * B**(-1)
phi = (x[0,1]/x[0,0]*e1).floor()
try:
d = inverse_mod( 65537, phi)
m = hex(power_mod(c, d, N))[2:]
if m.startswith('44415343'):
print(i)
print(bytes.fromhex(m))
break
except:
pass给定3组
类似2组情况,其中
$b=[k_1k_2k_3,d_1gk_2k_3,k_1d_2gk_3,d_1d_2g^2k_3,k_1k_2d_3g,k_1d_3g,k_2d_3g,d_1d_2d_3g^3]$
$L_3=\left[\begin{matrix} 1-N & 0 & N^2 & 0 & 0 & 0 & -N^3 \newline e_1 & -e_1 & -e_1N & -e & 0 & e_1N & e_1N^2 \newline 0 & e_2 & -e_2N & 0 & e_2N & 0 & e_2N^2 \newline 0 & 0 & e_1e_2 & 0 & -e_1e_2 & -e_1e_2 & -e_1e_2N \newline 0 & 0 & 0 & e_3 & -e_3N & -e_3N & e_3N^3 \newline 0 & 0 & 0 & 0 & e_1e_3 & 0 & -e_1e_3N \newline 0 & 0 & 0 & 0 & 0 & e_2e_3 & -e_2e_3N \newline 0 & 0 & 0 & 0 & 0 & 0 & e_1e_2e_3 \end{matrix}\right] \times D$
其中 $D={\rm diag}(N^{3/2},N,N^{(3/2)+\alpha_3},N^{1/2},N^{(3/2)+\alpha_3},N^{1+\alpha_3},N^{1+\alpha_3},1)$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42from sage.all import *
import gmpy2
N =
e1 =
e2 =
e3 =
c =
for i in range(1000):
alpha2 = i/1000
M1 = int(gmpy2.mpz(N)**(3./2))
M2 = int( gmpy2.mpz(N) )
M3 = int(gmpy2.mpz(N)**(3./2 + alpha2))
M4 = int( gmpy2.mpz(N)**(0.5) )
M5 = int( gmpy2.mpz(N)**(3./2 + alpha2) )
M6 = int( gmpy2.mpz(N)**(1.+alpha2) )
M7 = int( gmpy2.mpz(N)**(1.+alpha2) )
D = diagonal_matrix(ZZ, [M1, M2, M3, M4, M5, M6, M7, 1])
B = Matrix(ZZ, [ [1, -N, 0, N**2, 0, 0, 0, -N**3],
[0, e1, -e1, -e1*N, -e1, 0, e1*N, e1*N**2],
[0, 0, e2, -e2*N, 0, e2*N, 0, e2*N**2],
[0, 0, 0, e1*e2, 0, -e1*e2, -e1*e2, -e1*e2*N],
[0, 0, 0, 0, e3, -e3*N, -e3*N, e3*N**2],
[0, 0, 0, 0, 0, e1*e3, 0, -e1*e3*N],
[0, 0, 0, 0, 0, 0, e2*e3, -e2*e3*N],
[0, 0, 0, 0, 0, 0, 0, e1*e2*e3] ]) * D
L = B.LLL()
v = Matrix(ZZ, L[0])
x = v * B**(-1)
phi_ = (e1*x[0,1]/x[0,0]).floor()
try:
d = inverse_mod( 65537, phi_)
m = hex(power_mod(c, d, N))[2:]
if m.startswith('44415343'):
print(i)
print(bytes.fromhex(m))
break
except:
pass给定更多组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236from Crypto.Util.number import *
isdigit = lambda x: ord('0') <= ord(x) <= ord('9')
def my_permutations(g, n):
sub = []
res = []
def dfs(s, prev):
if len(s) == n:
res.append(s[::])
for i in g:
if i in s or i < prev:
continue
s.append(i)
dfs(s, max(prev, i))
s.remove(i)
dfs(sub, 0)
return res
class X3NNY(object):
def __init__(self, exp1, exp2):
self.exp1 = exp1
self.exp2 = exp2
def __mul__(self, b):
return X3NNY(self.exp1 * b.exp1, self.exp2 * b.exp2)
def __repr__(self):
return '%s = %s' % (self.exp1.expand().collect_common_factors(), self.exp2)
class X_Complex(object):
def __init__(self, exp):
i = 0
s = '%s' % exp
while i < len(s):
if isdigit(s[i]):
num = 0
while i < len(s) and isdigit(s[i]):
num = num*10 + int(s[i])
i += 1
if i >= len(s):
self.b = num
elif s[i] == '*':
self.a = num
i += 2
elif s[i] == '/':
i += 1
r = 0
while i < len(s) and isdigit(s[i]):
r = r*10 + int(s[i])
i += 1
self.b = num/r
else:
i += 1
if not hasattr(self, 'a'):
self.a = 1
if not hasattr(self, 'b'):
self.b = 0
def WW(e, d, k, g, N, s):
return X3NNY(e*d*g-k*N, g+k*s)
def GG(e1, e2, d1, d2, k1, k2):
return X3NNY(e1*d1*k2- e2*d2*k1, k2 - k1)
def W(i):
e = eval("e%d" % i)
d = eval("d%d" % i)
k = eval("k%d" % i)
return WW(e, d, k, g, N, s)
def G(i, j):
e1 = eval("e%d" % i)
d1 = eval("d%d" % i)
k1 = eval("k%d" % i)
e2 = eval("e%d" % j)
d2 = eval("d%d" % j)
k2 = eval("k%d" % j)
return GG(e1, e2, d1, d2, k1, k2)
def R(e, sn): # min u max v
ret = X3NNY(1, 1)
n = max(e)
nn = len(e)
l = set(i for i in range(1, n+1))
debug = ''
u, v = 0, 0
for i in e:
if i == 1:
ret *= W(1)
debug += 'W(%d)' % i
nn -= 1
l.remove(1)
u += 1
elif i > min(l) and len(l) >= 2*nn:
ret *= G(min(l), i)
nn -= 1
debug += 'G(%d, %d)' % (min(l), i)
l.remove(min(l))
l.remove(i)
v += 1
else:
ret *= W(i)
l.remove(i)
debug += 'W(%d)' % i
nn -= 1
u += 1
# print(debug, end = ' ')
return ret, u/2 + (sn - v) * a
def H(n):
if n == 0:
return [0]
if n == 2:
return [(), (1,), (2,), (1, 2)]
ret = []
for i in range(3, n+1):
ret.append((i,))
for j in range(1, i):
for k in my_permutations(range(1, i), j):
ret.append(tuple(k + [i]))
return H(2) + ret
def CC(exp, n):
cols = [0 for i in range(1<<n)]
# split exp
texps = ('%s' % exp.exp1.expand()).strip().split(' - ')
ops = []
exps = []
for i in range(len(texps)):
if texps[i].find(' + ') != -1:
tmp = texps[i].split(' + ')
ops.append(0)
exps.append(tmp[0])
for i in range(1, len(tmp)):
ops.append(1)
exps.append(tmp[i])
else:
ops.append(0)
exps.append(texps[i])
if exps[0][0] == '-':
for i in range(len(exps)):
ops[i] = 1-ops[i]
exps[0] = exps[0][1:]
else:
ops[0] = 1
# find e and N
l = []
for i in range(len(exps)):
tmp = 1 if ops[i] else -1
en = []
j = 0
while j < len(exps[i]):
if exps[i][j] == 'e':
num = 0
j += 1
while isdigit(exps[i][j]):
num = num*10 + int(exps[i][j])
j += 1
tmp *= eval('e%d' % num)
en.append(num)
elif exps[i][j] == 'N':
j += 1
num = 0
if exps[i][j] == '^':
j += 1
while isdigit(exps[i][j]):
num = num*10 + int(exps[i][j])
j += 1
if num == 0:
num = 1
tmp *= eval('N**%d' % num)
else:
j += 1
if tmp == 1 or tmp == -1:
l.append((0, ()))
else:
l.append((tmp, tuple(sorted(en))))
# construct h
mp = H(n)
for val, en in l:
cols[mp.index(en)] = val
#print(cols)
return cols
def EWA(n, elist, NN, alpha):
mp = H(n)
var('a')
S = [X_Complex(n*a)]
cols = [[1 if i == 0 else 0 for i in range(2^n)]]
for i in mp[1:]:
eL, s = R(i, n)
cols.append(CC(eL, n))
S.append(X_Complex(s))
alphaA,alphaB = 0, 0
for i in S:
alphaA = max(i.a, alphaA)
alphaB = max(i.b, alphaB)
#print(alphaA, alphaB)
D = [int(NN^((alphaA-S[i].a)*alpha + (alphaB - S[i].b))) for i in range(len(S))]
#print(D)
kw = {'N': NN}
for i in range(len(elist)):
kw['e%d' % (i+1)] = elist[i]
print(cols)
B = Matrix(ZZ, Matrix(cols).T(**kw)) * diagonal_matrix(ZZ, D)
L = B.LLL(0.5)
v = Matrix(ZZ, L[0])
x = v * B**(-1)
phi = int(x[0,1]/x[0,0]*elist[0])
return phi
def attack(NN, elist, alpha):
phi = EWA(len(elist), elist, NN, alpha)
print(phi)
elist = [ ]
NN=
alpha = 400./2048
for i in range(1, len(elist)+1):
var("e%d" % i)
var("d%d" % i)
var("k%d" % i)
g, N, s = var('g'), var('N'), var('s')
for i in range(len(elist)):
elist[i] = Integer(elist[i])
attack(NN, elist, alpha)
phi =
c=
d=inverse(65537,int(phi))
m = pow(c,d,NN)
print(long_to_bytes(int(m)))参考Paper
Common Modulus Attacks on Small Private Exponent RSA and Some Fast Variants (in Practice)
Extending Wiener’s Attack in the Presence of Many Decrypting Exponents
多项式RSA
在整数RSA原理基础上将多项式代入分析:
在有限域上选取两个不可约多项式 $g(p),g(q)$,$g(n)=g(p) \cdot g(q)$,计算出 $g(n)$ 的欧拉函数 $\varphi(g(n))=\varphi$,
选取一个整数 $e$ 作为公钥,$e$ 与 $\varphi$ 是互素的,那么对于明文 $g(m)$,加密过程为 $g(m)^e \equiv g(c) \pmod {g(n)}$,
计算私钥 $d$ 满足 $ed \equiv 1 \pmod \varphi$,则 $g(c)^d \equiv (g(m)^e)^d \equiv g(m)^{ed} \equiv g(m)^{\varphi+1} \pmod {g(n)}$,
同样考虑 $g(n)$ 与 $g(m)$ 互素,欧拉定理对于多项式亦成立,
得到 $g(m)^{\varphi+1} \equiv g(m) \pmod {g(n)}$,所以 $g(c)^d \equiv g(m) \pmod {g(n)}$。
显然RSA对于整数的体制可以适用于有限域上的多项式。
★注意:
对于素数 $x$,$\varphi(x)=x-1$,但是对于不可约多项式 $g(x)$,$\varphi(g(x))=p^n-1$。(此 $p$ 为 $GF(p)$ 的模,此 $n$ 为多项式最高项次数)
原因:
由欧拉函数定义本身,欧拉函数是小于 $n$ 的所有与 $n$ 互质的数的个数。
多项式的欧拉函数则类似,表示不高于 $g(x)$ 幂级的环内所有多项式中,与 $g(x)$ 无公因式(非1)的其他多项式的个数,所以每一个不高于 $g(x)$ 幂级的环内多项式(除了它自己)均满足此条件。
1 | #脚本1 |
1 | #脚本2 |
1 | #Sage |
参考:
Crypto CTF2020 - Decent RSA
SecurityFest CTF 2022 - small rsa
Weak prime factors (p具线性特征)
适用情况:$p$ 满足 $ap=u_0+M_1u_1+\cdots+M_ku_k$
先根据 $n$ 确定 $M$ 的大小,再根据 $M$ 选取符合要求的 $k$ 和 $c$,然后构造一个格如下:
$M(\mathcal{L})=\begin{bmatrix}{1}&{0}&{0}&{\cdots}&{0}&{CM^{2k}} \newline
{0}&{1}&{0}&{\cdots}&{0}&{CM^{2k-1}} \newline {\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots} \newline {0}&{0}&{0}&{\cdots}&{1}&{CM} \newline {0}&{0}&{0}&{\cdots}&{0}&{-CN} \newline \end{bmatrix}$
用LLL算法进行格基规约,将规约后的某个向量作为多项式系数,再对多项式进行分解,即可完成对 $n$ 的分解。
参考
Factoring RSA moduli with weak prime factors
N1CTF2020 - easyRSA
1 | from tqdm import tqdm |
p多次幂因子
适用情况:$N=p^rq$
情形1
条件:$(N,e)$ 满足 $ex-\varphi(N)y=z$,其中 $x$ 与 $\lvert z \rvert$ 为小参数。
$f(x) = ex-z \equiv 0 \pmod {p^{r-1}}$
计算 $\gcd(ex - z,N)=g$,则
$p = \begin{cases} g^{\frac{1}{r-1}},\text{if } g=p^{r-1} \newline g^{\frac{1}{r}},\text{if } g=p^{r} \newline \frac{N}{g},\text{if } g=p^{r-1}q \end{cases}$
1
2
3
4P.<x> = PolynomialRing(Zmod(n))
f = e * x - b
root = f.monic().small_roots(X=2**672,beta=0.75)[0]
g = gcd(int(e * root - b),n3)情形2
条件:小 $\lvert d_1-d_2 \rvert$,$\lvert d_1-d_2 \rvert \lt N^{\frac{r(r-1)}{(r+1)^2}}$。
$f(x) = e_1e_2(d_1-d_2) - (e_2-e_1) \equiv 0 \pmod {p^{r-1}}$
等价于 $g(x) = x-a \equiv 0 \pmod {p^{r-1}}$,其中 $a \equiv (e_2-e_1)(e_1e_2)^{-1} \pmod {N}$。
计算 $\gcd(e_1e_2x - (e_2-e_1),N)=g$,则
$p = \begin{cases} g^{\frac{1}{r-1}},\text{if } g=p^{r-1} \newline g^{\frac{1}{r}},\text{if } g=p^{r} \newline \frac{N}{g},\text{if } g=p^{r-1}q \end{cases}$
1
2
3
4P.<x> = PolynomialRing(Zmod(n))
f = e1*e2*x - e1 + e2
root = f.monic().small_roots(X=2**672,beta=0.75)[0]
g = gcd(int(e1*e2*root - e1 + e2),n)情形3
条件:$N_1=p_1^rq_1,N_2=p_2^rq_2$,小 $\lvert p_1-p_2 \rvert$,$\lvert p_1-p_2 \rvert \lt \cfrac{p_1}{2rq_1q_2}$。
$\left| \cfrac{N_2}{N_1} - \cfrac{q_2}{q_1} \right| = \cfrac{q_1q_2 \lvert p_1^r - p_2^r \rvert}{q_1^2p_1^r} < \cfrac{1}{2q_1^2}$
利用 $\cfrac{N_2}{N_1}$ 的连分数展开对应的渐进分数逼近 $\cfrac{q_2}{q_1}$。
1
2
3
4
5
6
7
8
9
10
11
12
13cf = continued_fraction(n1/n2)
fracs = cf.convergents()
for xx in tqdm(fracs):
q1 = xx.numerator()
q2 = xx.denominator()
if q1.nbits() in range(511, 513) and q2.nbits() in range(511, 513):
if n1 % q1 == 0:
print(q1)
assert n1 % q1 == 0
p1 = int((n1 // q1)^(1/2))
p2 = int((n2 // q2)^(1/2))
assert p1^2 * q1 == n1
break
参考:
New attacks on RSA with Moduli $N = p^rq$
D^3CTF 2022 - d3factor
RSA-CRT
故障注入攻击
RSA-CRT fault attack
假设在计算 $S_q$ 时发生了错误,$S_q=m_q^{d_q} \bmod q$,$m_q=m \bmod q$,$d_q=d \bmod (q-1)$,
正确签名:$S=S_p \cdot(q^{-1} \bmod p) \cdot q+S_q \cdot(p^{-1} \bmod q) \cdot p$,
错误签名:$\hat{S} = S_p \cdot (q^{-1} \bmod p) \cdot q + \hat{S_q} \cdot (p^{-1} \bmod q) \cdot p$,
则 $S - \hat{S} = (S_q - \hat{S_q}) \cdot (p^{-1} \bmod q) \cdot p$,即有 $p=\gcd(S-\hat{S},N)$。
或由错误签名 $\hat{S}$,有 $p=\gcd(S’^e-m,N)$。
错误模攻击
有明文 $m$ 经对应编码后的 $\sigma_p = \mu(m)^d \bmod p, \sigma_q = \mu(m)^d \bmod q$,生成RSA-CRT签名 $\sigma = (\sigma_p\cdot\alpha + \sigma_q\cdot\beta) \bmod N$,其中参数 $\alpha = q \cdot (q^{-1} \bmod p),\beta = p \cdot (p^{-1} \bmod q)$。
利用错误模注入技术得到错误签名 $\sigma’$,即 $\sigma’ = (\sigma_p\cdot\alpha + \sigma_q\cdot\beta) \bmod N’$,
对生成的两种签名 $\sigma$ 和 $\sigma’$ 使用CRT可计算出 $v=(\sigma_p\cdot\alpha + \sigma_q\cdot\beta) \bmod (N \cdot N’)$。
针对 $l \ge 5$ 的编码后消息进行分析,通过计算签名对 $(\sigma,\sigma’)$ 分解 $N$ 的攻击方法:
对所有的 $i$,计算出对应的整数 $v_i= \text{CRT}_{N,N’}(\sigma_i,\sigma_i’)$,这些对应的 $v_i$ 构成 $\mathbb{Z}^l$ 上的向量 $\mathbf{v}=(v_1,\cdots,v_i)$;
利用LLL定理计算出垂直于向量 $\mathbf{v}$ 的正交格 $\mathbf{v}^{\perp}$ 的规约基 $\mathbf{b}_1,\cdots,\mathbf{b}_{l-1}$,其中所有的向量和格的分布都是在 $\mathbb{Z}^l$ 内。通过对存在于 $\mathbb{Z}^{1+l}$ 中的格应用LLL定理,即对如下矩阵使用LLL定理:
$\begin{pmatrix} kv_1 & 1 & & 0 \newline \vdots& & \ddots & \newline kv_l & 0 & & 1 \end{pmatrix}$
其中 $k$ 为合适的大常量,并去除计算出来的向量的第1个元素;
前 $l-2$ 个向量 $\mathbf{b}_1,\cdots,\mathbf{b}_{l-2}$ 将生成秩为 $l-2$ 的格 $L’$,再次利用LLL定理来计算出正交格 $(L’)^{\perp}$ 的规约基 $\mathbf{x}’,\mathbf{y}’$。同样可以通过对如下矩阵使用LLL定理得到对应的规约基:
$\begin{pmatrix} k’b_{1,1} & \cdots & k’b_{l-2,1} & 1 & & 0 \newline \vdots& & \vdots & & \ddots & \newline k’b_{1,l} & \cdots & k’b_{l-2,l}& 0 & & 1 \end{pmatrix}$
同步骤2,保留计算出来的向量的最后 $l$ 个元素;
将所有长度不超过 $\sqrt{lN}$ 的并在 $(L’)^{\perp}$ 内的向量 $\mathbf{z}=a \mathbf{x}’+b \mathbf{y}’$ 列举出来,对符合条件的向量 $\mathbf{z}$,计算出 $\gcd(\mathbf{v}-\mathbf{z},N)$,可以得出 $N$ 中任何可能的素因子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28from tqdm import tqdm
import gmpy2,sys
def orthogonal_lattice(B):
LB = B.transpose().left_kernel(basis="LLL").basis_matrix()
return LB
cs = []
s = []
l = 6
v = []
for i in range(len(cs_)):
v.append(int(crt([s_[i], cs_[i]], [n, N])))
v = vector(ZZ, v)
Lv = orthogonal_lattice(Matrix(v))
L1 = orthogonal_lattice(Lv.submatrix(0, 0, l-2, l))
x, y = L1
for a in tqdm(range(333)):
for b in tqdm(range(333)):
z = a*x+b*y
for each in (v-z):
tmp = gcd(each,n)
if tmp>1:
p = tmp
print(p)
sys.exit()参考:
Modulus Fault Attacks Against RSA-CRT Signatures
2022巅峰极客 - Learning with Fault
矩阵RSA
对于有限域 $\mathbb{F}_p$ 上的 $n \times n$ 矩阵构成的一般线性群 $\text{GL}(n,\mathbb{F}_p)$,其阶数可以通过以下公式计算:
$\vert\text{GL}(n,\mathbb{F}_p)\vert=(p^n-1)(p^n-p)(p^n-p^2)\cdots(p^n-p^{n-1})$
其他特别情形
多素数因子(Multi-prime RSA)
$n=p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m} \\ \Rightarrow \begin{eqnarray}\varphi(n) &=&\varphi(p_1^{k_1})\varphi(p_2^{k_2}) \cdots \varphi(p_m^{k_m}) \\ &=&(p_1^{k_1-1}\cdot(p_1-1))(p_2^{k_2-1}\cdot(p_2-1)) \cdots (p_m^{k_m-1}\cdot(p_m-1)) \end{eqnarray}$
next_prime()
根据素数定理,素数的平均间隔为:$\cfrac{x}{\pi(x)} \approx \ln(x)$,因此常见的下一个素数比当前素数大一点,一般不会超过1500。
变种1:$n=p \cdot q \cdot \text{nextprime}(p) \cdot \text{nextprime}(q)$
给 e,p,c
$c \equiv m^e \pmod n \\\Leftrightarrow c_1 \equiv c \pmod p \equiv m^e \pmod p$
令 $ed_1 \equiv 1 \pmod {(p-1)}$,有 $m \equiv c^d \pmod n \equiv c_1^{d_1} \pmod p$。
给 e,d,modinv(q,p),c
已知:$p,q$ 同比特位数。
令 $cf=q^{-1} \bmod p$,有 $q\cdot cf=1 \pmod p$。
$ed=1+k(p-1)(q-1)$,
比较比特位数,$k$ 与 $e$ 同长,可爆破 $k$,得 $\varphi(n)=(p-1)(q-1)=\cfrac{ed-1}{k}$;
上式 $\varphi(n) =(p-1)(q-1) \pmod p=-(q-1) \pmod p$,
结合 $q\cdot cf=1 \pmod p$,即 $q\cdot cf-1=0 \pmod p$,
联立:
$\begin{eqnarray} \varphi(n)&=&(p-1)(q-1)\\&=&pq-p-q+1\\&=&n-p-q+1 \end{eqnarray}$
$\begin{eqnarray} cf\cdot \varphi(n)&=&cf\cdot(n-p-q+1)\\&=&cf\cdot n-cf\cdot p-cf\cdot q+cf \end{eqnarray}$
$\begin{eqnarray} cf\cdot \varphi(n) \bmod p&=&(cf\cdot n-cf\cdot p-cf\cdot q+cf) \bmod p\\&=&0-0-(cf\cdot q)+cf \bmod p\\&=&-1+cf \bmod p \end{eqnarray}$
有 $1+cf\cdot \varphi(n)-cf=0\pmod p$,
即$x=1+cf\cdot \varphi(n)-cf$ 能被 $p$ 整除;
由费马小定理,存在 $r$ 满足 $r^{p-1}=1 \pmod p$,
$\begin{eqnarray}r^{\varphi(n)}&=&(r^{(p-1)})^{(q-1)}\\&=&1^{(q-1)} \pmod p\\&=&1 \pmod p \end{eqnarray}$,
因对于任意 $r,k_1,k_2$,当 $k_2$ 为 $k_1$ 因子时,$r \bmod k_2=(r \bmod k_1) \bmod k_2$,
故 $r^{\varphi(n)} \bmod p=(r^{\varphi(n)} \bmod x) \bmod p=1 \bmod p=kp$,
已知 $\varphi(n)$,由 $(r^{\varphi(n)} \bmod x) \bmod p=kp$ 可得到多组 $p$ 的乘积,计算 $\gcd$ 可得到 $p$;
由 $q\cdot cf=1 \pmod p$ 求模逆可得 $q$,再用 $c$ 计算出 $m$。
gcd(e,φ(n)) ≠ 1
$\gcd(e,\varphi(n))\neq 1$ 时,$e$ 与 $\varphi(n)$ 不互素,
$m^e \equiv (m^{\gcd(e,\varphi(n))})^{\frac{e}{\gcd(e,\varphi(n))}} \equiv c \pmod n$,计算 $\frac{e}{\gcd(e,\varphi(n))}$ 的模逆 $d’$,
则 $c^{d’}\equiv m^{\gcd(e,\varphi(n))}\pmod n$。
当 $\gcd(e,\varphi(n))$ 较小时,可以直接对 $c$ 开根,有两种情况:
- $m^e = c<n$,这种情况直接对 $c$ 开 $e$ 次方即可;
- $m^e = c>n$,这种情况需要在有限域下对 $c$ 开方,一般先计算 $c_p=c \bmod p$,$c_q=c \bmod q$,分别求出 $c_p,c_q$ 在 $c$ 下的 $e$ 次根(可能有多个),然后使用CRT遍历所有组合,分别check得出明文。
当 $\gcd(e,\varphi(n))$ 较大时,求 $p,q$ 的 $e$ 次根步骤需要替换为一些有限域开根的高效算法(如AMM算法等)进行计算。
也可以:
假设 $\gcd(e,\varphi(n)) = k$,计算 $d= \text{inv}\Big(e, \cfrac{\varphi(n)}{k}\Big)$。
参考:
e|(p-1), e|(q-1)
上面的 $\gcd(e,\varphi(n))\neq 1$ 情况不针对 $\gcd(e,\varphi(n))= e$,这里对 $e\mid (p-1),e\mid (q-1)$ 的特殊情况进行讨论。
解题思路即求解 $m \bmod p$ 和 $m \bmod q$ ,再通过CRT还原 $m \bmod n$。主要难点则是在 $\text{GF}(p)$ 上求 $e$ 次根。
在有限域上求r-th root有两个常见算法(Adleman-Manders-Miller algorithm和Cipolla-Lehmer algorithm),Namhun Koo提出一种更具一般性的开根算法,且在 $s$ 足够小的时候更高效($r^{s}\mid (p-1),r^{s}\nmid (p-1)$)。
★参考:NCTF 2019 - easyRSA (Adleman-Manders-Miller rth Root Extraction Method)
本题则为 $e$ 和 $p-1$ (或 $q-1$)的最大公约数就是 $e$ 本身,也就是说 $e\mid (p-1)$,只有对 $c$ 开 $e$ 次方根才行。
可以将同余方程 $m^e \equiv c \pmod n$ 化成
$\begin{cases} m^e \equiv c \pmod p \\ m^e \equiv c \pmod q \end{cases}$
然后分别在 $\text{GF}(p)$ 和 $\text{GF}(q)$ 上对 $c$ 开 $e$ 次方根,再用CRT组合一下即可得到在 $\bmod n$ 下的解。
问题是,如何在有限域内开根?
这里 $e$ 与 $p-1$ 和 $q-1$ 都不互素,不能简单地求个逆元就完事。
这种情况下,开平方根可以用
Tonelli–Shanks algorithm,Wiki说这个算法可以扩展到开n次方根。在这篇paper里给出了具体的算法:
Adleman-Manders-Miller rth Root Extraction Method。这个算法只能开出一个根,实际上开 $e$ 次方,最多会有 $e$ 个根(这题的情况下有0x1337个根)。
如何找到其他根?
StackOverflow – Cube root modulo P 给出了方法。
如何找到所有的
primitive 0x1337th root of 1?StackExchange – Finding the n-th root of unity in a finite field 给出了方法。
Exploit(以
e=0x1337 为例)- 先用
Adleman-Manders-Miller rth Root Extraction Method在 $\text{GF}(p)$ 和 $\text{GF}(q)$ 上对 $c$ 开 $e$ 次方根,分别得到一个解。大概不到10秒。 - 然后去找到所有的
0x1336个primitive nth root of 1,乘以上面那个解,得到所有的0x1337个解。大概1分钟。 - 再用CRT对 $\text{GF}(p)$ 和 $\text{GF}(q)$ 上的两组
0x1337个解组合成 $\bmod n$ 下的解,可以得到0x1337**2=24196561个 $\bmod n$ 的解。最后能通过check()的即为flag。大概十几分钟。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16#脚本1
#Sage
c =
p =
q =
e =
for mp in GF(p)(c).nth_root(e, all=True):
for mq in GF(q)(c).nth_root(e, all=True):
m = crt([ZZ(mp), ZZ(mq)], [p, q])
try:
res = bytes.fromhex(hex(m)[2:])
if res.isascii():
print(res)
except:
pass1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109#脚本2
#Sage
import random
import time
# About 3 seconds to run
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(a, d)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c ^ r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def findAllPRoot(p, e):
print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p))
start = time.time()
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
end = time.time()
print("Finished in {} seconds.".format(end - start))
return proot
def findAllSolutions(mp, proot, cp, p):
print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p))
start = time.time()
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
end = time.time()
print("Finished in {} seconds.".format(end - start))
return all_mp
c =
p =
q =
e = 0x1337
cp = c % p
cq = c % q
mp = AMM(cp, e, p)
mq = AMM(cq, e, q)
p_proot = findAllPRoot(p, e)
q_proot = findAllPRoot(q, e)
mps = findAllSolutions(mp, p_proot, cp, p)
mqs = findAllSolutions(mq, q_proot, cq, q)
print(mps, mqs)
def check(m):
h = m.hex()
if len(h) & 1:
return False
if bytes.fromhex(h).startswith(b'NCTF'):
print(bytes.fromhex(h))
return True
else:
return False
# About 16 mins to run 0x1337^2 == 24196561 times CRT
start = time.time()
print('Start CRT...')
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if check(solution):
print(solution)
print(time.time() - start)
end = time.time()
print("Finished in {} seconds.".format(end - start))
- 先用
SMUPE 问题(不同N,e加密线性关系明文)
a system of univariate polynomial equations problem = 一元多项式方程组求解问题
定义
$k$ 是一个整数,$N$ 为满足RSA算法的模数,$\delta$ 是多项式的阶。有
$N_i<N_{i+1},\delta_i \in N\quad(i=1,2,\cdots,k)$
多项式方程组表示如下, 目的是求解 $x$:
$\begin{cases} f_1(x)\equiv 0 \pmod {N_1}\newline f_2(x)\equiv 0 \pmod {N_2} \newline {\vdots} \newline f_k(x)\equiv 0 \pmod {N_k} \end{cases}$
求解条件
Alexander May, Maike Ritzenhofent提出一种求解方法,简单地说当多项式的阶 $\delta$ 满足以下情况时可解($\delta$ 是多项式的阶):
$\sum\limits_{i=1}^k \cfrac{1}{\delta_i} \geq 1$
具体描述:
令 $(f_i,\delta_i,N_i) \quad(i=1,2,\cdots,k)$ 作为SMUPE问题的首一多项式组,
定义 $M=\prod\limits_{i=1}^k N_i^{\frac{\delta}{\delta_i}},\delta=\text{lcm}(\delta_i) \quad (i=1,2,\cdots,k)$
则SMUPE问题可以在 $O(\delta^6\cdot \log_2M)$ 复杂度解决。
反素数(emirp数)
已知:$q=\text{reverse_x}(p)$,$\text{x}$ 为进制数。
爆破思路类似RSA parity oracle。$p,q$ 是bit翻转关系,已知 $p$ 最低的 $k$ 位,则已知 $q$ 最高的 $k$ 位。
假设已知 $k$ 位的 $p,q$,记为 $ph,qh$,利用不等式
$ph\cdot qh\cdot 2^{1024-2k}<=n<(ph+1)\cdot(qh+1)\cdot 2^{1024-2k}$ ,
逐位向低地址爆破,不断收缩不等式的范围,最终可求得 $n$ 值。
参考:
RoarCTF 2020 - Reverse
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29#python2
#x=10
n = 6528060431134312098979986223024580864611046696815854430382374273411300418237131352745191078493977589108885811759425485490763751348287769344905469074809576433677010568815441304709680418296164156409562517530459274464091661561004894449297362571476259873657346997681362092440259333170797190642839587892066761627543
def t(a, b, k):
# sqrt(n) has 155 digits, so we need to figure out 77 digits on each side
if k == 77:
if a*b == n:
print a, b
return
for i in xrange(10):
for j in xrange(10):
# we try to guess the last not-already-guessed digits of both primes
a1 = a + i*(10**k) + j*(10**(154-k))
b1 = b + j*(10**k) + i*(10**(154-k))
if a1*b1 > n:
# a1 and b1 are too large
continue
if (a1+(10**(154-k)))*(b1+(10**(154-k))) < n:
# a1 and b1 are too small
continue
if ((a1*b1)%(10**(k+1))) != (n%(10**(k+1))):
# The last digits of a1*b1 (which won't change later) doesn't match n
continue
# this a1 and b1 seem to be a possible match, try to guess remaining digits
t(a1, b1, k+1)
# the primes have odd number of digits (155), so we try all possible middle digits (it simplifies the code)
for i in xrange(10):
t(i*(10**77), i*(10**77), 0)
4p-1 method
对使用一类特定素数乘积的模数的分解。
当一类特殊的素数用在 RSA 模数中时,可以轻易的将该素数从 $n$ 中分解出来。由于这一类素数都形如 $4p−1=Ds^2$,因此又被称为
4p-1 method。此外,有些人也会将其视为 RSA 的后门之一,称之为RSA backdoor。QiCheng Prime
$Ds=\{3,11,19,43,67,163\}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28import sys
sys.setrecursionlimit(10^6)
def QiCheng(n):
R = Integers(n)
attempts = 20
js = [0, (-2^5)^3, (-2^5*3)^3, (-2^5*3*5)^3, (-2^5*3*5*11)^3, (-2^6*3*5*23*29)^3]
for _ in range(attempts):
for j in js:
if j == 0:
a = R.random_element()
E = EllipticCurve([0, a])
else:
a = R(j)/(R(1728)-R(j))
c = R.random_element()
E = EllipticCurve([3*a*c^2, 2*a*c^3])
x = R.random_element()
z = E.division_polynomial(n, x)
g = gcd(z, n)
if g > 1:
return g
n =
p = int(QiCheng(Integer(n)))Masaaki Shirase & Vladimir Sedlacek Improvement
更多 $Ds$ 值。
参考:
NCTF 2020 - RSA_revenge
CryptoHack Challenge - RSA Backdoor Viability
Common Prime RSA
情形:$\gcd(p-1,q-1)=g$
分解的n方法有四种:
(1)修改Pollard’s rho方法分解n;
(2)知道a、b的值分解n;
(3)知道g的值分解n;
(4)分解N-1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25# Pollard’s rho
from Crypto.Util.number import *
import gmpy2
def f(x, n):
return (pow(x, n - 1, n) + 3) % n
def rho(n):
i = 1
print 'Factorizing'
while True:
x1 = getRandomRange(2, n)
x2 = f(x1, n)
j = 1
while True:
p = gmpy2.gcd(abs(x1 - x2), n)
if p == n:
break
elif p > 1 and isPrime(p):
print 'Found!'
return (p, n // p)
else:
x1 = f(x1, n)
x2 = f(f(x2, n), n)
j += 1
i += 1
RSA Padding Oracle Attack
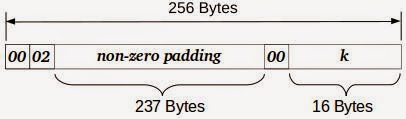
RSA PKCS #1 v1.5 填充用于需要RSA加密的信息,为了加密K,消息首先被0x00、一些随机字节和0x00 0x02填充,随机字节的选择方式是为了让填充的信息达到特定的块长度(1024、2048或4096位)。
PKCS #1 v1.5 标准中可以伪造RSA签名。
Bleichenbacher攻击
可以识别在
0x00 02后以明文开始的密文信息,然后进行Padding Oracle攻击来解密预主密钥,进一步可以取得SSL的会话密钥。充分利用
0x00 02开头的特性,假设攻击者获得密文 $C_0$,想恢复出明文 $M_0$。攻击方法是通过向服务器多次发送修改后的密文,分析响应是正确还是错误来确定修改结果,进而解密信息。如果收到正确,则表示是
0x00 02开头,那么 $2B \lt m \lt 3B-1$,且 $B=2^{8(L-2)}$,而且基于RSA加密的延展性,可得 $C=(C_0S)\bmod N=(M_0S)^e \bmod N$ ,攻击者可用 $C$ 进行查询,如果收到错误则增加 $S$,并重复上一步骤。攻击者可以利用
0x00 02大幅度减少可能的取值,$2B \lt M_0S-rN \lt 3B$,因此攻击者能够降低范围$\cfrac{2B+rN}{S} \lt M_0 \lt \cfrac{3B+rN}{S}$,然后迭代选择 $S$,进行Oracle查询,计算新的 $r$ 值,攻击者便可以不断缩小包含 $M_0$ 的范围,不断重复直到最后只剩唯一解。参考:
Chosen Ciphertext Attacks Against Protocols Based on the RSA Encryption Standard PKCS #1
Bleichenbachers “Million Message Attack” on RSA
Pwnhub - pkcs_fix
Return of Coppersmith’s attack (ROCA)
CVE-2017-15361
形如 $p=kM+(65537^a \bmod M)$ 生成素数的RSA系统,$M$ 是前 $n$ 个连续素数的乘积,$n$ 是仅取决于所需密钥大小的常数。
https://github.com/jvdsn/crypto-attacks/blob/master/attacks/factorization/roca.py
PEM密钥
由-----BEGIN <TAG>-----开头,-----END <TAG>-----结尾,中间是Base64编码的一串二进制,每64个字母(即解码后的48bytes)有一个换行。中间的Base64解码后是一串遵循ASN.1协议的DER编码,简单来说可以看成一种序列化,把一个结构体中的整数、字串等编码成一个方便传输的二进制。
生成代码:
1 | from Crypto.PublicKey import RSA |
RSA私钥
1 | -----BEGIN RSA PRIVATE KEY----- |
RFC3447定义:
1 | RSAPrivateKey ::= SEQUENCE { |
例:
1 | 3082025d02010002818100a0d154d5bf97c40f7797b44819d09c608fa4b5c38e70d83bc13267138c6eff4c1aacefe3ddb571e1b41d911c7ab6136cf90493189563450e1f4270cabbc4207c54c4da7b84a20311cfbbabe82b9fe60bdf48a08d57839d0cdf9464d84262bcc06bc308095a6987f60ad07d669a312b5a7e4133213788eecf25863248b91349ef02030100010281800f8270c496903bf3e3ec4912450f15edc81cb1fcf4b154615aee11fbd428e64d402b5a8d66d5f770358f3e6df935b324e8d5349c83d7c992a5982249a31734acb1db19c4c8d829267514bc1ef7bbfbe242d4350f67a002a56d33e56d1a94adc71c68f020dc39ab7d0064c111b164e26ba0698dc94a03cdfd516ffd966e877949024100ca97e49c058237f96e99118ce383f91912cba1163de9236181ff754ef3ef1a260fac8d2d9aee866d51a8b6836983b05cf850e786289b6859925bc8695fc67c47024100cb3630aafffcb29607f0833dc7f05c143ee92fadfe975da4cf6719e71226bee72562e8631328a25d7351507a8d43c1295ab6ea242b60a28b109233a983f4211902401b4a32a541a8b4d988a85dd0d8a4e25d1a470bbfef3f0461121dd3337b706dd94aab37a9390180622169d48c071e921733ebd204245c2ac6460ccf0642bc7de90241008d9f44a7c823eaaa58fa2bdd20bcc8cf6b50c463f4acb51ca956e75c7ceff7d7cbdc74aca7ab880cacd39cccec2aae320e00b0896899be6e40ac43c8fe2763f1024100c67ca6d988f53abea82159431a146512a8d942978d4a8f83f2d426f1095e3bf1b5b9b8b1ccbbad2a31c6401880447a45f5e0790269061ac13b5f68f1777d7f07 |
30是Sequence的tag,82是指接下来后两个bytes是这个Sequence的长度,即0x025d个bytes,也就是剩下全部都是;接着的020100就是整数0,其中02是整数的tag,01是这个整数占1byte,00是value同样的方法也可以解02818100a0...和后面其他整数,拆分:
1 | 3082025d # Begin Sequence: len=0x025d |
RSA公钥
1 | -----BEGIN PUBLIC KEY----- |
例:
1 | 30819f300d06092a864886f70d010101050003818d0030818902818100a0d154d5bf97c40f7797b44819d09c608fa4b5c38e70d83bc13267138c6eff4c1aacefe3ddb571e1b41d911c7ab6136cf90493189563450e1f4270cabbc4207c54c4da7b84a20311cfbbabe82b9fe60bdf48a08d57839d0cdf9464d84262bcc06bc308095a6987f60ad07d669a312b5a7e4133213788eecf25863248b91349ef0203010001 |
拆分:
1 | 30819f # Begin Main Sequence: len=0x9f |
参考

